§ 24. Приклади застосування методу координат у фізиці
У попередньому розділі розглянуто, що коли обрано конкретний базис, існує взаємно однозначна відповідність між векторами та їх координатами 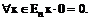 .
.
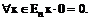 та функцій цих чисел. Такий спосіб вивчення векторних величин називають методом координат. Він є надзвичайно цінним для фізики та інженерної справи, оскільки врешті-решт результат дії більшості (якщо не всіх) фізичних приладів та технічних контролюючих пристроїв полягає у визначенні певних чисел (як у випадку, наприклад, цифрового вольтметра) або числових функцій скалярного аргументу (як у випадку осцилографа чи будь-якого приладу, до якого підключено самописець). Коли ці числа перетворюються при переході від однієї системи відліку до іншої за допомогою співвідношень
та функцій цих чисел. Такий спосіб вивчення векторних величин називають методом координат. Він є надзвичайно цінним для фізики та інженерної справи, оскільки врешті-решт результат дії більшості (якщо не всіх) фізичних приладів та технічних контролюючих пристроїв полягає у визначенні певних чисел (як у випадку, наприклад, цифрового вольтметра) або числових функцій скалярного аргументу (як у випадку осцилографа чи будь-якого приладу, до якого підключено самописець). Коли ці числа перетворюються при переході від однієї системи відліку до іншої за допомогою співвідношень 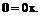 подібних до (2.10), їх можна вважати координатами вектора x. Не буде перебільшенням сказати, що у фізиці поняття координати є первинним, а поняття вектора похідним від нього. Для пояснення цієї думки наведемо конкретні приклади з різних галузей фізики. · Механіка
подібних до (2.10), їх можна вважати координатами вектора x. Не буде перебільшенням сказати, що у фізиці поняття координати є первинним, а поняття вектора похідним від нього. Для пояснення цієї думки наведемо конкретні приклади з різних галузей фізики. · Механіка Вектори фазового простору. Розглянемо механічну систему, що описується декартовими або кутовими координатами  та відповідними імпульсами
та відповідними імпульсами  де
де  – функція Лагранжа (різниця кінетичної та потенціальної енергій системи),
– функція Лагранжа (різниця кінетичної та потенціальної енергій системи),  S – кількість ступенів вільності.
S – кількість ступенів вільності.
 означеними у такий спосіб:
означеними у такий спосіб: 
Множина всіх векторів x утворює 2S-вимірний фазовий простір механічної системи. У конкретному випадку системи N незв'язаних матеріальних точок вимірність фазового простору дорівнює 6N.
4-вектори. Важливими поняттями релятивістської механіки є поняття 4-радіус-вектора та 4-імпульса матеріальної точки (елементарної частинки), які означаються як вектори з координатами  та
та

відповідно. (Тут x, y, z – координати радіус-вектора частинки в геометричному просторі, t – момент часу в який визначається її просторове положення,  та p – енергія та звичайний імпульс частинки, c – швидкість світла). Ці вектори широко застосовуються, наприклад, у фізиці високих енергій, оскільки вони дуже спрощують описання процесів зіткнення елементарних частинок. Спрощення пов'язане з тим, що в таких процесах зберігається (лишається сталою) величина
та p – енергія та звичайний імпульс частинки, c – швидкість світла). Ці вектори широко застосовуються, наприклад, у фізиці високих енергій, оскільки вони дуже спрощують описання процесів зіткнення елементарних частинок. Спрощення пов'язане з тим, що в таких процесах зберігається (лишається сталою) величина  де
де  Дійсно, враховуючи відомі релятивістські формули для енергії та імпульсу частинки з масою спокою m та швидкістю v
Дійсно, враховуючи відомі релятивістські формули для енергії та імпульсу частинки з масою спокою m та швидкістю v

легко помітити, що за будь-яких значень швидкості частинки  а тому, як би не відбувалося зіткнення даної частинки з іншою частинкою, її 4-імпульс змінитися не може. · Електродинаміка
а тому, як би не відбувалося зіткнення даної частинки з іншою частинкою, її 4-імпульс змінитися не може. · Електродинаміка
Для спрощення рівнянь електродинаміки часто вводять до розгляду поняття 4-потенціала та 4-струму.
Ці величини означаються як вектори з координатами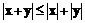 та
та  відповідно. Координати цих векторів мають такий фізичний зміст: А – векторний потенціал, пов'язаний з магнітним полем H рівністю
відповідно. Координати цих векторів мають такий фізичний зміст: А – векторний потенціал, пов'язаний з магнітним полем H рівністю 
 – скалярний потенціал, який визначається з рівняння
– скалярний потенціал, який визначається з рівняння

 – густина електричного заряду, j – густина струму.
– густина електричного заряду, j – густина струму.
За допомогою 4-потенціалу та 4-струму вдається спростити запис законів електродинаміки. Наприклад, закон збереження заряду у підручниках із загальної фізики зазвичай подають у вигляді рівняння неперервності

а в курсі теоретичної фізики часто записують еквівалентне до нього рівняння

яке є стислим записом закону збереження заряду.
Підкреслимо, що в усіх наведених вище прикладах простий фізичний зміст мають координати векторів, а самі вектори слід розглядати як суто формальні поняття, введення яких у розгляд спрощує математичне описання механічних систем. · Квантова теорія
Серйозне вивчення квантової теорії в її сучасному формулюванні можливе лише після ознайомлення з повним університетським курсом лінійної алгебри. Оскільки вище було викладено лише початкові розділи цього курсу, зараз можна лише спробувати охарактеризувати в загальних рисах місце поняття векторного простору у загальній будові квантової механіки.
В основі квантової механіки лежить поняття стаціонарного стану фізичної системи, як такого її стану, який характеризується певними значеннями фізичних величин.
Серед цих величин найважливішою є енергія, тому для визначеності будемо говорити про стаціонарні енергетичні стани і вважатимемо, що енергія системи може набувати лише дискретних значень En , n = 1,2,3,... . Дозволені значення енергії називають енергетичними рівнями фізичної системи. Квантова теорія вивчає системи як з обмеженою, так і з нескінченою кількістю рівнів.Згідно з основними постулатами квантової механіки кожному енергетичному стану можна поставити у відповідність вектор стану, причому для векторів стану є справедливим принцип суперпозиції, за яким лінійні комбінації векторів стану також є векторами станів. Таким чином, вектори стану утворюють векторний простір .
Далі, усі енергетичні стани поділяються на два типи. Якщо фізична система перебуває в енергетичному стані першого типу, можна стверджувати, що в результаті вимірювання її енергії буде одержано одне з дозволених значень енергії En. (Вектори станів першого типу звичайно позначають символом  ). Натомість, для станів другого типу існує ймовірність одержання декількох із дозволених значень енергії. З формального точки зору різниця між станами двох типів пояснюється таким чином. Вектори
). Натомість, для станів другого типу існує ймовірність одержання декількох із дозволених значень енергії. З формального точки зору різниця між станами двох типів пояснюється таким чином. Вектори  енергетичних станів першого типу утворюють базис у просторі . Це означає, що довільний вектор простору може бути поданий у вигляді розкладу за векторами базису:
енергетичних станів першого типу утворюють базис у просторі . Це означає, що довільний вектор простору може бути поданий у вигляді розкладу за векторами базису:

Вектори  , для яких розклад містить більше одного доданка, відповідають станам другого типу. Імовірність отримання в результаті вимірювання значення енергії En дорівнює квадрату модуля відповідного коефіцієнта розкладу:
, для яких розклад містить більше одного доданка, відповідають станам другого типу. Імовірність отримання в результаті вимірювання значення енергії En дорівнює квадрату модуля відповідного коефіцієнта розкладу:  Отже, сума всіх величин
Отже, сума всіх величин  обов'язково має дорівнювати одиниці.
обов'язково має дорівнювати одиниці.