§ 17. Приклади лінійно залежних та лінійно незалежних векторів
2.30. Приклад. Нульовий вектор утворює систему лінійно залежних векторів 
Щоб упевнитися в цьому, досить утворити хоч одну нетривіальну лінійну комбінацію, яка дорівнює нулю.
Такою комбінацією є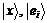
2.31. Приклад. Вектор  утворює систему лінійно незалежних векторів
утворює систему лінійно незалежних векторів 
Будь-яка лінійна комбінація векторів  має вигляд
має вигляд  Оскільки
Оскільки  з умови лінійної залежності
з умови лінійної залежності  випливає, що
випливає, що  Отже, єдина нульова лінійна комбінація векторів
Отже, єдина нульова лінійна комбінація векторів  – тривіальна.
– тривіальна.
2.32. Приклад. Два колінеарні геометричні вектори утворюють систему лінійно залежних векторів 
Із шкільного курсу геометрії відомо, що колінеарні вектори завжди пов'язані між собою рівністю  причому
причому  коли вектори напрямлені в один бік і
коли вектори напрямлені в один бік і  коли вони напрямлені в різні боки (нульовий вектор не має певного напрямку). Переписавши рівність у вигляді
коли вони напрямлені в різні боки (нульовий вектор не має певного напрямку). Переписавши рівність у вигляді  переконуємося в тому, що існує нетривіальна
переконуємося в тому, що існує нетривіальна  лінійна комбінація векторів системи.
лінійна комбінація векторів системи.
2.33.
Приклад. Два неколінеарні геометричні вектори утворюють систему лінійно незалежних векторів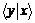
Припустимо протилежне: нехай вектори системи  лінійно залежні. Тоді існує нетривіальна лінійна комбінація
лінійно залежні. Тоді існує нетривіальна лінійна комбінація  Оскільки один із коефіцієнтів (для визначеності
Оскільки один із коефіцієнтів (для визначеності  ) не дорівнює нулю, вектори системи пов'язані рівністю
) не дорівнює нулю, вектори системи пов'язані рівністю  з якої випливає, що вони колінеарні, усупереч вихідному припущенню.
з якої випливає, що вони колінеарні, усупереч вихідному припущенню.