Основні поняття та визначення.
1.1. Означення. Матрицею розмірів  , (тут
, (тут  ) назвемо сукупність
) назвемо сукупність  виразів, розташованих у вигляді таблиці з m стрічок та n стовпчиків.
виразів, розташованих у вигляді таблиці з m стрічок та n стовпчиків.
 =
= 
Вирази, які складають матрицю, називаються елементами матриці. В загальному випадку елементи матриці можуть мати довільну природу – це можуть бути дійсні або комплексні числа, символи, функції і т.д.
Якщо число стрічок в матриці дорівнює числу стовпчиків, то матриця називається квадратною, а число стрічок – порядком матриці. Інші матриці носять назву прямокутних. Матриці складаються з m стрічок та n стовпчиків, тому їх часто називають  матрицями. Для
матрицями. Для  матриці
матриці  можна використовувати коротке позначення
можна використовувати коротке позначення  , а якщо розміри матриці обумовлено завчасно, то не вказуючи їх, будемо писати
, а якщо розміри матриці обумовлено завчасно, то не вказуючи їх, будемо писати  або
або  . Елементи матриці позначають буквами з двома індексами: aij або ai j, Якщо два індекси розташовані внизу, то перший з них означає номер стрічки, а другий – номер стовпчика, на перетині яких розташований даний елемент матриці.
. Елементи матриці позначають буквами з двома індексами: aij або ai j, Якщо два індекси розташовані внизу, то перший з них означає номер стрічки, а другий – номер стовпчика, на перетині яких розташований даний елемент матриці.
1.2. Зауваження. Для матриць, ялементами яких є дійсні або комплексні числа (числові матриці) справедливим є і таке означення – розглянемо дві множини цілих чисел:  та
та  Через
Через  позначимо множину всіх пар чисел виду
позначимо множину всіх пар чисел виду  , де
, де  – число з множини I, j - число з множини J. Матрицею називається функція на множині
– число з множини I, j - число з множини J. Матрицею називається функція на множині  , тобто закон, який співставляє кожній парі
, тобто закон, який співставляє кожній парі  деяке число
деяке число  .
.
1.3. Означення. Дві матриці  і
і  називають рівними, якщо вони мають одинакові розміри (кількість стовпчиків і стрічок матриць співпадають) і їх елементи, які стоять на однакових місцях, є рівними:
називають рівними, якщо вони мають одинакові розміри (кількість стовпчиків і стрічок матриць співпадають) і їх елементи, які стоять на однакових місцях, є рівними:  .
.
1.4. Означення. Нехай  і
і  – матриці, які складаються з m стрічок і n стовпчиків. Сумою матриць
– матриці, які складаються з m стрічок і n стовпчиків. Сумою матриць  і
і  називають матрицю
називають матрицю  тих же розмірів
тих же розмірів  , кожен елемент якої дорівнює сумі елементів матриць
, кожен елемент якої дорівнює сумі елементів матриць  та
та  , які стоять на тих же місцях, тобто елементи
, які стоять на тих же місцях, тобто елементи  матриці
матриці  пов’язані з елементами
пов’язані з елементами  та
та  матриць
матриць  та
та  рівністю
рівністю
 для всіх
для всіх  ;
;  .
.
Суму матриць  та
та  позначають
позначають  .
.
1.5. Зауваження. Операція “сума матриць” визначена тільки для матриць одних і тих же розмірів!
1.6. Означення. Матриця  , елементи якої
, елементи якої  дорівнюють добутку елементів
дорівнюють добутку елементів  матриці
матриці  на дійсне або комплексне число α називається добутком матриці
на дійсне або комплексне число α називається добутком матриці  на число α і позначається
на число α і позначається  . Маємо
. Маємо
 для всіх
для всіх  ;
;  .
.
З означень 1.3. і 1.4. витікають наступні властивості операцій додавання матриць  і
і  одних і тих же розмірів та множення матриці на довільні числа α і β.
одних і тих же розмірів та множення матриці на довільні числа α і β.
1.7. Властивість. Додавання матриць є комутативною операцією, тобто  .
.
1.8. Властивість. Додавання матриць є асоціативною операцією:
 .
.
1.9. Властивість. Множення матриці на число є дистрибутивною операцією по відношенню до додавання чисел: 
1.10.
Властивість. Множення матриці на число є дистрибутивною операцією по відношенню до додавання матриць: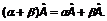
1.11. Властивість. Множення матриці на число – асоціативна операція: 
1.12. Означення. Матриця, всі елементи якої дорівнюють нулю, називається нульовою матрицею. Якщо  – нульова матриця розмірів
– нульова матриця розмірів  , то для любої матриці
, то для любої матриці  тих же розмірів маємо
тих же розмірів маємо  .
.
1.13. Означення. Матрицю (-1) називають протилежною до матриці
називають протилежною до матриці  і позначаємо
і позначаємо  . Матриця, протилежна до заданої матриці, має властивість
. Матриця, протилежна до заданої матриці, має властивість 
1.14. Означення. Операція віднімання матриць визначається через операції додавання матриць та множення матриці на число, тобто сума матриць  і
і  називається різницею матриць
називається різницею матриць  та
та  і позначається
і позначається 
1.15. Означення. Квадратна матриця довільного порядку n всі “n” елементи якої розташовані на головній діагоналі і дорівнюють 1, а всі інші елементи дорівнюють нулю, називається одиничною і позначається  .
.
1.16. Означення. Матрицю розмірів  , тобто таку, яка складається з однієї стрічки, називають матрицею-стрічною або вектор-стрічкою або просто стрічкою довжини n. Матрицю розмірів
, тобто таку, яка складається з однієї стрічки, називають матрицею-стрічною або вектор-стрічкою або просто стрічкою довжини n. Матрицю розмірів  , яка складається з одного стовпчика, називають матрицею-стовпчиком або вектор-стовпчиком висоти m або просто стовпчиком.
, яка складається з одного стовпчика, називають матрицею-стовпчиком або вектор-стовпчиком висоти m або просто стовпчиком.
В подальшому зручно застосовувати позначення векторів-стовпчиків і векторів-стрічок, уперше запропоновані Полем Діраком. Зручність цих позначень полягає в тому, що вектор-стовпчик 
 важко переплутати з вектор-стрічкою
важко переплутати з вектор-стрічкою  , а добуток матриць
, а добуток матриць , що є числом, з добутком
, що є числом, з добутком  , який є матрицею порядку n (операцію множення матриць буде означено пізніше) Позначення Дірака широко застосовуються в сучасній літературі з квантової механіки, квантової теорії поля, квантової оптики, фізики твердого тіла тощо.
, який є матрицею порядку n (операцію множення матриць буде означено пізніше) Позначення Дірака широко застосовуються в сучасній літературі з квантової механіки, квантової теорії поля, квантової оптики, фізики твердого тіла тощо.
Матрицю  =
=  довільних розмірів
довільних розмірів  можна розглядати як сукупність стовпчиків висоти m або сукупність стрічок довжини n. Нехай
можна розглядати як сукупність стовпчиків висоти m або сукупність стрічок довжини n. Нехай  , тоді матрицю
, тоді матрицю  можна записати у такому вигляді
можна записати у такому вигляді  . Аналогічно, якщо
. Аналогічно, якщо
 ,
,
тоді та ж матриця запишеться у такому вигляді  =
= .
.
1.17. Зауваження. Операцію додавання векторів-стрічок визначено для векторів-стрічок однієї довжини, так само як додавання векторів-стовпчиків – тільки для векторів-стовпчиків однієї висоти. Для цих двох видів матриць ми детальніше вивчимо операції додавання і множення на число. При цьому мова буде йти тільки про вектори-стовпчики, так як для векторів-стрічок всі властивості формуються і доводяться аналогічно.
1.18. Означення. Вектор-стовпчик  називається лінійною комбінацією стовпчиків
називається лінійною комбінацією стовпчиків  однакової висоти, якщо при деяких числах α1 , …, αm
однакової висоти, якщо при деяких числах α1 , …, αm  або більш детально
або більш детально

Числа  називають коефіцієнтами лінійної комбінації. В силу означень операцій множення матриці на число та додавання ця рівність рівносильна числовим рівностям
називають коефіцієнтами лінійної комбінації. В силу означень операцій множення матриці на число та додавання ця рівність рівносильна числовим рівностям

1.19. Означення. Вектор-стовпчик, всі елементи якого дорівнюють нулеві, називається нульовим і позначається наступним чином  . Аналогічно визначається і нульова вектор-стрічка
. Аналогічно визначається і нульова вектор-стрічка 
1.20. Означення. Система з s стовпчиків  однієї і тієї ж висоти називається лінійно незалежною, якщо з рівності
однієї і тієї ж висоти називається лінійно незалежною, якщо з рівності

слідує  . В противному випадку система з s стовпчиків є лінійно залежною.
. В противному випадку система з s стовпчиків є лінійно залежною.
1.21. Означення. Лінійну комбінацію вектор-стовпчиків, всі s коефіцієнтів якої дорівнюють нулеві, називають тривіальною. З допомогою цього терміну означення 1.20. можна сформулювати так: система стовпчиків є лінійно залежною, якщо існує рівна нульовому стовпчику нетривіальна лінійна комбінація цих стовпчиків. Система стовпчиків є лінійно незалежною тоді і тільки тоді, коли тільки тривіальна лінійна комбінація цих стовпчиків дорівнює нульовому стовпчику.
1.22. Приклад. Лінійно незалежною системою вектор-стовпчиків є наступна система з n вектор-стовпчиків:

1.23. Властивість. Система з s > 1 стовпчиків лінійно залежна тоді і тільки тоді, коли хоча б один з стовпчиків є лінійною комбінацією інших стовпчиків.
 Нехай система є лінійно залежною. Тоді, згідно означенню 1.20., існує нетривіальна лінійна комбінація системи векторів-стовпчиків, що розглядаються, рівна нульовому вектор-стовпчику:
Нехай система є лінійно залежною. Тоді, згідно означенню 1.20., існує нетривіальна лінійна комбінація системи векторів-стовпчиків, що розглядаються, рівна нульовому вектор-стовпчику:

Нехай який-небудь з коефіцієнтів  Звідси
Звідси

тобто j-тий стовпчик є лінійною комбінацією інших стовпчиків. Навпаки, якщо один з стовпчиків є лінійною комбінацією інших, тобто має місце рівність  то з цієї рівності слідує існування нетривіальної лінійної комбінації векторів з відмінними від нуля коефіцієнтами, рівної нульовому вектору
то з цієї рівності слідує існування нетривіальної лінійної комбінації векторів з відмінними від нуля коефіцієнтами, рівної нульовому вектору
1.24. Властивість. Якщо система векторів утримує нульовий вектор стовпчик, то система є лінійно залежною.
 Дійсно, любий нульовий стовпчик є тривіальна лінійна комбінація довільної системи вектор-стовпчиків, тобто доведення цієї властивості зводиться до доведення попередньої властивості.
Дійсно, любий нульовий стовпчик є тривіальна лінійна комбінація довільної системи вектор-стовпчиків, тобто доведення цієї властивості зводиться до доведення попередньої властивості.
1.25. Властивість. Якщо деякі з стовпчиків даної системи  утворюють самі по собі лінійно залежну підсистему стовпчиків, то і вся система є лінійно залежною.
утворюють самі по собі лінійно залежну підсистему стовпчиків, то і вся система є лінійно залежною.
 В силу сформульованого, існує нетривіальна лінійна комбінація деякої підсистеми заданої системи стовпчиків, рівна нульовому стовпчику. Якщо до цієї комбінації стовпчиків додати інші стовпчики заданої системи з нульовими коефіцієнтами, то отримаємо нетривіальну лінійну комбінацію всіх стовпчиків, яка дорівнює нульовому стовпчику.
В силу сформульованого, існує нетривіальна лінійна комбінація деякої підсистеми заданої системи стовпчиків, рівна нульовому стовпчику. Якщо до цієї комбінації стовпчиків додати інші стовпчики заданої системи з нульовими коефіцієнтами, то отримаємо нетривіальну лінійну комбінацію всіх стовпчиків, яка дорівнює нульовому стовпчику.
1.26. Властивість. Любі стовпчики, які входять в лінійно незалежну систему стовпчиків, самі по собі утворюють лінійно незалежну систему.
 Якби було не так, то ми прийшли б до протиріччя з попередньою властивістю.
Якби було не так, то ми прийшли б до протиріччя з попередньою властивістю.
1.27. Властивість. Якщо стовпчик  є лінійна комбінація стовпчиків
є лінійна комбінація стовпчиків  , які є підсистемою деякої системи стовпиків
, які є підсистемою деякої системи стовпиків  , то
, то  є також лінійною комбінацією цієї системи стовпчиків.
є також лінійною комбінацією цієї системи стовпчиків.
Для доведення до даної лінійної комбінації підсистеми достатньо добавити ті стовпчики системи стовпчиків, яких не вистачає, з нульовими коефіцієнтами.
1.28. Властивість. Любий стовпчик  висоти n є лінійною комбінацією стовпчиків
висоти n є лінійною комбінацією стовпчиків 
Дійсно, яким би не був стовпчик  , лінійна комбінація стовпчиків
, лінійна комбінація стовпчиків  з коефіцієнтами, які співпадають з відповідними елементами заданої матриці, дорівнює заданій матриці
з коефіцієнтами, які співпадають з відповідними елементами заданої матриці, дорівнює заданій матриці  :
:
 .
.
Розглянемо матрицю з m стрічок та n стовпчиків. Їй можна співставити матрицю  з n стрічок та m стовпчиків за наступним правилом: елементи кожньої стрічки матриці
з n стрічок та m стовпчиків за наступним правилом: елементи кожньої стрічки матриці  записуються в тому ж порядку в стовпчики матриці
записуються в тому ж порядку в стовпчики матриці  , причому номер стовпчика співпадає є номером стрічки, тобто
, причому номер стовпчика співпадає є номером стрічки, тобто  -та стрічка матриці
-та стрічка матриці  складається з тих же елементів і в тому ж порядку, що й
складається з тих же елементів і в тому ж порядку, що й  -ий стовпчик матриці
-ий стовпчик матриці 
 .
.
Таку матрицю називають транспонованою по відношенню до  і позначають
і позначають  , перехід від
, перехід від  до
до  називають транспонуванням. Визначення транспонованої матриці можна записати у вигляді
називають транспонуванням. Визначення транспонованої матриці можна записати у вигляді  рівностей:
рівностей:  ,
,  ,
,  ,...,
,...,  ,...,
,...,  , які зв’язують елементи матриці
, які зв’язують елементи матриці  і
і  для всіх
для всіх  ,
,  .
.
1.29. Приклад. Матриці  ,
,  і
і  називається матрицями Паулі і відіграють надзвичайно важливу роль в квантовій механіці і квантовій теорії поля.
називається матрицями Паулі і відіграють надзвичайно важливу роль в квантовій механіці і квантовій теорії поля.
Для цих матриць маємо
 ,
,  і
і  .
.
Очевидно,  ,
,  і
і  .
.
1.30. Означення. Матриці, для яких справедливо  , називаються симетричними, а матриці для яких
, називаються симетричними, а матриці для яких  , називаються антисиметричними. Матриці
, називаються антисиметричними. Матриці  і
і  є симетричними, а матриця
є симетричними, а матриця  є антисиметричною.
є антисиметричною.