§ 6. Елементарні перетворення як множення матриць. Детермінант добутку.
1.72. Теорема. Кожне елементарне перетворення стрічок матриці А розмірів  рівносильно множенню матриці А зліва на деяку квадратну матрицю порядку m.
рівносильно множенню матриці А зліва на деяку квадратну матрицю порядку m.
 Розглянемо квадратну матрицю
Розглянемо квадратну матрицю 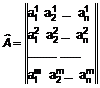 , яка отримується з одиничної матриці
, яка отримується з одиничної матриці  порядку
порядку  перестановкою і-ої та j–ої стрічок. Очевидно, що при множенні матриці
перестановкою і-ої та j–ої стрічок. Очевидно, що при множенні матриці  розмірів
розмірів  зліва на
зліва на 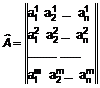 відповідні стрічки матриці А переставляться.
відповідні стрічки матриці А переставляться.
Нехай 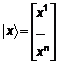 – матриця, яка отримується з тієї ж одиничної матриці
– матриця, яка отримується з тієї ж одиничної матриці  заміною і-ої одиниці на діагоналі на число
заміною і-ої одиниці на діагоналі на число  . При множенні матриці А зліва на
. При множенні матриці А зліва на 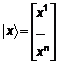 і-а стрічка матриці А помножиться на
і-а стрічка матриці А помножиться на  .
.
Позначимо через 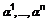 матрицю, яка отримується з одиничної матриці
матрицю, яка отримується з одиничної матриці  заміною на одиницю нульового елемента, розташованого на перетині і-ої стрічки та j–го стовпчика.
заміною на одиницю нульового елемента, розташованого на перетині і-ої стрічки та j–го стовпчика.
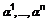 рівносильно додаванню j–ої стрічки матриці А до і-ої стрічки. Зауважимо, що
рівносильно додаванню j–ої стрічки матриці А до і-ої стрічки. Зауважимо, що 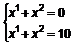 ,
, 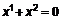 i
i 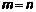 відмінні від нуля:
відмінні від нуля: 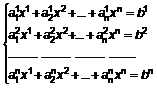 ,
, 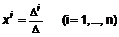 ,
, 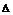 . Матриці
. Матриці 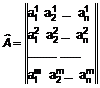 ,
, 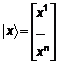 і
і 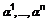 називають матрицями елементарних перетворень. Якщо матриця А квадратна, то
називають матрицями елементарних перетворень. Якщо матриця А квадратна, то 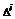 ,
, 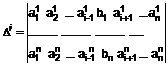 ,
, 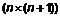 отже в цьому випадку для матриць елементарних перетворень справедливо
отже в цьому випадку для матриць елементарних перетворень справедливо 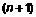 .
. Послідовному виконанню елементарних перетворень стрічок матриці відповідає множення зліва на добуток відповідних матриць елементарних перетворень. Елементарні перетворення стовпчиків можемо довести, домножаючи матрицю А справа на аналогічні матриці.
1.73. Припущення. Якщо  , то знайдуться матриці елементарних перетворень
, то знайдуться матриці елементарних перетворень  такі, що
такі, що  .
.
Якщо  , то
, то  існує. Так як
існує. Так як  , то елементарними перетвореннями стрічок матриця
, то елементарними перетвореннями стрічок матриця  може бути перетворена в одиничну матрицю, тобто знайдуться такі
може бути перетворена в одиничну матрицю, тобто знайдуться такі  , для яких
, для яких  . Очевидно, що
. Очевидно, що  .
.
1.74. Зауваження. Існування оберненої матриці для кожної невиродженої матриці буде доведено в наступному параграфі.
1.75. Припущення. Для любих квадратних матриць А і В одного порядку  .
.
 Дійсно, у випадку
Дійсно, у випадку  твердження витікає з оцінки рангу добутку матриць. Якщо
твердження витікає з оцінки рангу добутку матриць. Якщо  , то
, то
 →
→ 



в силу  .
.