§ 2. Детермінант матриці
1.31. Зауваження. Поняття «Детермінант» («Визначник») означено тільки для квадратних матриць. Детермінінт матриці позначається  , або, якщо потрібно виписати елементи цієї матриці – прямими рисками по боках цієї матриці.
, або, якщо потрібно виписати елементи цієї матриці – прямими рисками по боках цієї матриці.
1.32. Означення. Детермінант квадратної матриці – це число або символ, які їй ставляться у відповідність і можуть бути знайдені за елементами матриці згідно наступним означенням:
1) Детермінантом матриці порядку 1 називається єдиний елемент цієї ж матриці 
2) Детермінант матриці  порядку n > 1 називається число або символ, які наступним чином визначаються через елементи матриці
порядку n > 1 називається число або символ, які наступним чином визначаються через елементи матриці

де  детермінант матриці порядку (
детермінант матриці порядку ( ), яка отримується з матриці А викреслюванням її першої стрічки і k-го стовпчика.
), яка отримується з матриці А викреслюванням її першої стрічки і k-го стовпчика.
 називається додатковим мінором елемента
називається додатковим мінором елемента  заданої квадратної матриці. По аналогії можна визначити додатковий мінор
заданої квадратної матриці. По аналогії можна визначити додатковий мінор довільного елемента
довільного елемента  як детермінант матриці порядку (
як детермінант матриці порядку ( ), яка отримана з початкової матриці А викреслюванням тієї ж стрічки і того ж стовпчика, в яких розташовано елемент
), яка отримана з початкової матриці А викреслюванням тієї ж стрічки і того ж стовпчика, в яких розташовано елемент  , тобто
, тобто  –ої стрічки та
–ої стрічки та  -го стовпчика.
-го стовпчика.
1.33. Приклад. Користуючись означенням 1.32 знайдемо визначник матриць Паулі:



Властивості детермінантів
1.34. Властивість. Для кожної матриці А порядку n має місце формула
 ,
,
яка називається розкладом детермінанта за першим стовпчиком.
 Для доведення скористаємось методом математичної індукції.
Для доведення скористаємось методом математичної індукції.
Розглянемо визначник матриці другого порядку: 
 .
.
Вважаючи, що наступна рівність  , де А – матриця порядку (
, де А – матриця порядку ( ), є справедливою, отримаємо з неї основне співвідношення. Розкладемо визначник матриці порядку n за першою стрічкою, виділивши в сумі явно перший член:
), є справедливою, отримаємо з неї основне співвідношення. Розкладемо визначник матриці порядку n за першою стрічкою, виділивши в сумі явно перший член:

При любому  матриця, яка отримується з матриці А порядку n викреслюванням першої стрічки і k–ого стовпчика, утримує перший стовпчик без елемента
матриця, яка отримується з матриці А порядку n викреслюванням першої стрічки і k–ого стовпчика, утримує перший стовпчик без елемента  матриці А. Розкладемо
матриці А. Розкладемо  по цьому стовпчику, врахувавши, що i-та стрічка матриці А в
по цьому стовпчику, врахувавши, що i-та стрічка матриці А в  входить під номером (
входить під номером ( ), так як в
), так як в  не ввійшла перша стрічка матриці А.
не ввійшла перша стрічка матриці А.
Тому при  отримаємо
отримаємо  де
де  – детермінант матриці порядку
– детермінант матриці порядку  , яка отримується з
, яка отримується з  викреслюванням її
викреслюванням її  -ої стрічки та 1-го стовпчика, або, що те ж саме, викресленням з матриці
-ої стрічки та 1-го стовпчика, або, що те ж саме, викресленням з матриці  n-ого порядку 1-ої і і-ої стрічок та 1-го і k–го стовпчиків.
n-ого порядку 1-ої і і-ої стрічок та 1-го і k–го стовпчиків.
Тоді

Змінимо порядок сумування і винесемо множник, не залежний від k, за внутрішній знак суми.

Врахуємо, що  в силу того, що в матриці, детермінантом якої є
в силу того, що в матриці, детермінантом якої є  , в порівнянні з матрицею А пропущено перший стовпчик і всі номери стовпчиків зменшені на 1. Таким чином, маємо
, в порівнянні з матрицею А пропущено перший стовпчик і всі номери стовпчиків зменшені на 1. Таким чином, маємо
 =
=
1.35. Властивість. Для любої квадратної матриці  .
.
 Скористаємось знову методом математичної індукції. Для матриць другого порядку маємо:
Скористаємось знову методом математичної індукції. Для матриць другого порядку маємо:
 ,
,
 .
.
Вважаємо, що  . Тоді, використовуючи означення 1.36. для знаходження визначника матриці
. Тоді, використовуючи означення 1.36. для знаходження визначника матриці  та властивість 1.34. для знаходження визначника транспонованої матриці
та властивість 1.34. для знаходження визначника транспонованої матриці  , запишемо
, запишемо

 ,
,
де  - елементи першого стовпчика транспонованої матриці, тобто
- елементи першого стовпчика транспонованої матриці, тобто  . Враховуючи, що
. Враховуючи, що  , приходимо до рівності
, приходимо до рівності  .
.
1.37. Наслідок. З властивості 1.35. витікає рівноправність стрічок і стовпчиків – якщо справедливе яке-небудь твердження про детермінанти, яке має відношення до стрічок відповідної матриці, то є справедливим і аналогічне твердження, яке стосується стовпчиків. В силу цього наступні властивості достатньо довести тільки для стрічок.
1.38. Властивість. Якщо в квадратній матриці поміняти місцями які-небудь дві стрічки (два стовпчики), то детермінант матриці поміняє знак, не змінившись за абсолютніою величиною.
 Використовуємо для доведення метод математичної індукції
Використовуємо для доведення метод математичної індукції

 .
.
Припустимо, що твердження справедливе для матриць порядку ( ) і доведено його для матриць порядку n.
) і доведено його для матриць порядку n.
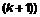 і
і 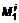 . Напишемо розклад визначника за першим стовпчиком, виділивши в ньому дві складові, які відповідають стрічкам, що переставляються
. Напишемо розклад визначника за першим стовпчиком, виділивши в ньому дві складові, які відповідають стрічкам, що переставляються  .
.
Аналогічно для матриці В, яка отримується з матриці А перестановкою k–ої і 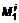 стрічок
стрічок
 .
.
При  ,
,  в
в  і
і  входять
входять  і
і  стрічки, але в різному порядку, а інші їх стрічки однакові, отже згідно припущенню індукції
стрічки, але в різному порядку, а інші їх стрічки однакові, отже згідно припущенню індукції  при
при  ,
,  . Матриці, детермінанти яких позначено
. Матриці, детермінанти яких позначено  і
і  співпадають – вони отримані викреслюванням
співпадають – вони отримані викреслюванням  стрічки з матриці В або, що те ж саме, k-ої стрічки матриці А. Тому
стрічки з матриці В або, що те ж саме, k-ої стрічки матриці А. Тому  =
= .
.
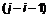 .
. Таким чином, порівнюючи  і
і  бачимо, що вони рівні за абсолютною величиною і відрізняються знаком. Нехай тепер в матриці А порядку n переставлено стрічки з номером і та j (
бачимо, що вони рівні за абсолютною величиною і відрізняються знаком. Нехай тепер в матриці А порядку n переставлено стрічки з номером і та j ( ). Перестановку і-ої та j-ої стрічок можна провести, переставляючи тільки сусідні стрічки: спочатку j–ту стрічку переставляємо послідовно з
). Перестановку і-ої та j-ої стрічок можна провести, переставляючи тільки сусідні стрічки: спочатку j–ту стрічку переставляємо послідовно з  стрічками, які стоять над нею (остання буде і-та), потім і-у стрічку переставляємо на j-те місце міняючи місцем з
стрічками, які стоять над нею (остання буде і-та), потім і-у стрічку переставляємо на j-те місце міняючи місцем з  стрічками, розташованими нижче від неї. Всього буде зроблено непарну
стрічками, розташованими нижче від неї. Всього буде зроблено непарну  кількість перестановок сусідніх стрічок. Так як при кожній з перестановок детермінант змінює знак, то в результаті знак детермінанту зміниться.
кількість перестановок сусідніх стрічок. Так як при кожній з перестановок детермінант змінює знак, то в результаті знак детермінанту зміниться.
Властивість 1.37. називають антисиметрією детермінанту відносно перестановок стрічок (стовпчиків).
Використовучи властивість антисиметрії можемо довести наступне.
1.39. Властивість. Для кожної квадратної матриці А порядку n при довільному і ( ) має місце співвідношення
) має місце співвідношення

і при довільному j ( )
)

Очевидно, при  перше співвідношення є означенням детермінанту.
перше співвідношення є означенням детермінанту.
Доведемо це співвідношення при  . Для цього переставимо і-ту стрічку на перше місце так, щоб не порушувати порядок інших стрічок, переставляючи і–ту стрічку послідовно з усіма стрічками, розташованими вище неї. Вище і-ої стрічки знаходиться
. Для цього переставимо і-ту стрічку на перше місце так, щоб не порушувати порядок інших стрічок, переставляючи і–ту стрічку послідовно з усіма стрічками, розташованими вище неї. Вище і-ої стрічки знаходиться  стрічка, Тому, якщо В – матриця, отримана з матриці
стрічка, Тому, якщо В – матриця, отримана з матриці  після перестановки
після перестановки  -ої стрічки на місце першої, то
-ої стрічки на місце першої, то  .
.
Розкладемо  по першій стрічці (і-ій стрічці матриці А)
по першій стрічці (і-ій стрічці матриці А)
 ,
,
де  – визначник матриці, яка отримується з матриці В викреслюванням першої стрічки і k-ого стовпчика, або, що те ж саме – з матриці А викреслюванням і-ої стрічки і k–ого стовпчика. Тому
– визначник матриці, яка отримується з матриці В викреслюванням першої стрічки і k-ого стовпчика, або, що те ж саме – з матриці А викреслюванням і-ої стрічки і k–ого стовпчика. Тому  . Враховуючи, що
. Враховуючи, що  , отримаємо
, отримаємо  .
.
1.40. Властивість. Якщо і-ий стовпчик (стрічка) матриці А є лінійна комбінація стовпчиків (стрічок)  та
та  , тобто має вигляд
, тобто має вигляд  де
де  і
і  – довільні числа, то
– довільні числа, то  , де матриці
, де матриці  і
і  отримуються з матриці А заміною її і-го стовпчика відповідно на стовпчики
отримуються з матриці А заміною її і-го стовпчика відповідно на стовпчики  і
і  .
.
Ця властивість носить назву лінійності детермінанта по стовпчику (стрічці).
 Дійсно, розкладемо визначник за і-тим стовпчиком і врахуємо
Дійсно, розкладемо визначник за і-тим стовпчиком і врахуємо  :
:

1.41. Зауваження. Цю властивість лінійності детермінанту по стовпчику можна сформулювати у вигляді двох окремих властивостей.
1). При множенні стовпчика матриці на число її детермінант множиться на це число.
2). Якщо стовпчик матриці є сумою двох стовпчиків, то її детермінант є сума детермінантів відповідних матриць.
1.42. Властивість. Якщо в матриці А стовпчики (стрічки) лінійно залежні, то її визначник дорівнює нулю.
 В першу чергу зауважимо, що якщо в матрицю входить нульовий рядок або нульовий стовпчик, то її визначник очевидно є рівним нулю. Крім цього, з властивості антисиметрії визначника слідує, що якщо матриця утримує два ідентичних рядки або стовпчики, то її визначник також дорівнює нулю. Якщо рядки в заданій матриці є лінійно залежними, то це означає, що хоча б один рядок (нехай його номер є
В першу чергу зауважимо, що якщо в матрицю входить нульовий рядок або нульовий стовпчик, то її визначник очевидно є рівним нулю. Крім цього, з властивості антисиметрії визначника слідує, що якщо матриця утримує два ідентичних рядки або стовпчики, то її визначник також дорівнює нулю. Якщо рядки в заданій матриці є лінійно залежними, то це означає, що хоча б один рядок (нехай його номер є  ) матриці є лінійною комбінацією інших рядків цієї матриці, тобто є справедливою наступна рівність:
) матриці є лінійною комбінацією інших рядків цієї матриці, тобто є справедливою наступна рівність:
 .
.
Тоді, розкладаючи визначник цієї матриці за і-тим рядочком і використовуючи властивість 1.39., отримуємо


де  – матриця, в якій на місці і-ого рядка знаходиться будь-який k-тий рядок цієї матриці, який не співпадає з і-тим рядком. Отже, кожна матриця
– матриця, в якій на місці і-ого рядка знаходиться будь-який k-тий рядок цієї матриці, який не співпадає з і-тим рядком. Отже, кожна матриця  утримує дві ідентичні стрічки, тому визначник кожної з цих матриць дорівнює нулю, тобто
утримує дві ідентичні стрічки, тому визначник кожної з цих матриць дорівнює нулю, тобто 