Вычисление вычетов
1.
Утв. Если  - устранимая особая точка
- устранимая особая точка  , то
, то  (Т.к.
(Т.к.
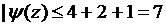 )
) 2.
а) Утв. Если  -простой полюс
-простой полюс  (полюс кратности 1), то
(полюс кратности 1), то  .
.
Док-во:


Пример.
 ,
, 
 имеет простой полюс.
имеет простой полюс.

б) Утв. Если  ,
, ,
, ,
, , то
, то  .
.
Док-во:
 -полюс I порядка
-полюс I порядка 

3.
Утв. Если  -полюс порядка n
-полюс порядка n  , то
, то  .
.
Док-во:




Переходим к  и делим на
и делим на  :
:

Пример1.
 ;
;
Пример2.

Лекция 9
Опр.  - изолированная особая точка
- изолированная особая точка  ,
,
 , где Г- замкнутый контур.
, где Г- замкнутый контур.
Утв. Если  , то
, то  .
.
Док-во:
1)  .
.
2) С: { }
}
 ,
, 
при 

3)

4) 

Теорема. Если  -изолированная особая точка, кроме
-изолированная особая точка, кроме  имеется конечное число особых точек, то
имеется конечное число особых точек, то 
Док-во:
Возьмем замкнутый контур С, охватывающий все особые точки, кроме 
 ;
;
 ;
;

 ;
;
Еще по теме Вычисление вычетов:
-
Аналитическая геометрия -
Вариационное исчисление -
Векторный и тензорный анализ -
Высшая геометрия -
Высшая математика -
Вычислительная математика -
Дискретная математика -
Дифференциальное и интегральное исчисление -
Дифференциальные уравнения -
Исследование операций -
История математики -
Комплексное исчисление -
Линейная алгебра -
Линейное программирование -
Математика для экономистов -
Математическая логика -
Математическая физика -
Математический анализ -
Пределы -
Ряды -
Статистика -
Теория вероятностей -
Теория графов -
Теория игр -
Теория принятия решений -
Теория случайных процессов -
Теория чисел -
Функциональный анализ -
-
Архитектура и строительство -
Безопасность жизнедеятельности -
Библиотечное дело -
Бизнес -
Биология -
Военные дисциплины -
География -
Геология -
Демография -
Диссертации России -
Естествознание -
Журналистика и СМИ -
Информатика, вычислительная техника и управление -
Искусствоведение -
История -
Культурология -
Литература -
Маркетинг -
Математика -
Медицина -
Менеджмент -
Педагогика -
Политология -
Право России -
Право України -
Промышленность -
Психология -
Реклама -
Религиоведение -
Социология -
Страхование -
Технические науки -
Учебный процесс -
Физика -
Философия -
Финансы -
Химия -
Художественные науки -
Экология -
Экономика -
Энергетика -
Юриспруденция -
Языкознание -