Связь между нулем и полюсом
Утв1. 
имеет в точке 
нуль порядка n 
имеет в точке полюс порядка n.
Док-во: {
}
Утв2. имеет существенно особую точку в точке имеет в неизолированную особую точку ИЛИ существенно особую точку.
Пример.
;
;
; 
;
Таким образом, получаем не изолированную особую точку.
Утв3. Если 
,
,
,
то имеет при:
1)m
n устранимую особую точку,
2)m>n полюс порядка n-m.
Док-во: {для 2}
;
Теорема Сохоцкого.
Если -существенно особая точка функции , то 
.
Док-во:
1)
а) 
-сходится при 
сходится при 
б) Предположим противное:
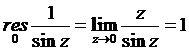ограничена в окрестности точки .
в) 
при 
(т.е.
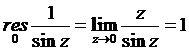ограничена в окрестности 
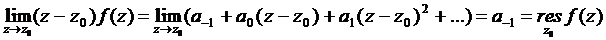). г)В круге 
ограничена, как непрерывная функция в замкнутой области.
д) Из б), в), г) следует ограничена на всей комплексной плоскости.
е) ограничена на С, аналитическая, по теореме Ляувилля 
противоречие.
2) 
а) 
имеет не изолированную особую точку.
б)
-изолированная особая точка
имеет изолированную особую точку в 
имеет существенно особую точку по Утв2 имеет существенно особую точку в
по 1) 
Теорема доказана.