24. Ряд Тейлора
Теорема22: пусть  -- аналитична в круге
-- аналитична в круге 
Тогда в этом круге наша функция раскладывается в степенной ряд, причём это разложение единственно
Про границу круга ничего не известно.
Поэтому проведём окружность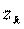 ,
, 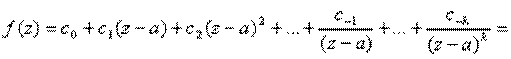 лежит внутри:
лежит внутри:  |  -- аналитична внутри Г и на Г, поэтому по интегральной формуле Коши имеем: -- аналитична внутри Г и на Г, поэтому по интегральной формуле Коши имеем:  |

 , и пусть
, и пусть  , тогда
, тогда 

Тогда 
Этот ряд равномерно сходится на  :
:  -- этот ряд сходится как геометрическая прогрессия с
-- этот ряд сходится как геометрическая прогрессия с  . Тогда по признаку Вейерштрасса, наш ряд
. Тогда по признаку Вейерштрасса, наш ряд  павномерно сходится на
павномерно сходится на 
Итак, 
Получим разложение по степеням, при этом 
Полученный ряд будет рядом Тейлора, поскольку коэффициенты считаются по такой формуле
Единственность доказывается элементарно
Теорема23 (неравенство Коши): пусть  -- аналитична в круге
-- аналитична в круге  .
.
 . Тогда
. Тогда  , где
, где  , где
, где 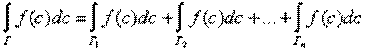
Доказательство: 
Тогда 
Источник:
Лекции по комплексным числам. 2016
Еще по теме 24. Ряд Тейлора:
-
Аналитическая геометрия -
Вариационное исчисление -
Векторный и тензорный анализ -
Высшая геометрия -
Высшая математика -
Вычислительная математика -
Дискретная математика -
Дифференциальное и интегральное исчисление -
Дифференциальные уравнения -
Исследование операций -
История математики -
Комплексное исчисление -
Линейная алгебра -
Линейное программирование -
Математика для экономистов -
Математическая логика -
Математическая физика -
Математический анализ -
Пределы -
Ряды -
Статистика -
Теория вероятностей -
Теория графов -
Теория игр -
Теория принятия решений -
Теория случайных процессов -
Теория чисел -
Функциональный анализ -
-
Архитектура и строительство -
Безопасность жизнедеятельности -
Библиотечное дело -
Бизнес -
Биология -
Военные дисциплины -
География -
Геология -
Демография -
Диссертации России -
Естествознание -
Журналистика и СМИ -
Информатика, вычислительная техника и управление -
Искусствоведение -
История -
Культурология -
Литература -
Маркетинг -
Математика -
Медицина -
Менеджмент -
Педагогика -
Политология -
Право России -
Право України -
Промышленность -
Психология -
Реклама -
Религиоведение -
Социология -
Страхование -
Технические науки -
Учебный процесс -
Физика -
Философия -
Финансы -
Химия -
Художественные науки -
Экология -
Экономика -
Энергетика -
Юриспруденция -
Языкознание -