Ряд Лорана
Теорема.  - аналитическая в кольце с центром
- аналитическая в кольце с центром  , то ее можно представить в виде ряда Ларана.
, то ее можно представить в виде ряда Ларана.


Док-во:




Г
Выберем точку z внутри кольца и окружности 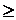 и Г (тоже внутри кольца), так чтобы точка z лежала между ними.
и Г (тоже внутри кольца), так чтобы точка z лежала между ними.

1. 
2. 
 Ряд мажорируется рядом
Ряд мажорируется рядом  Он сходится равномерно и его можно почленно интегрировать.
Он сходится равномерно и его можно почленно интегрировать.


Если контур С лежит между 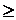 и Г, то интеграл по С равен интегралу по
и Г, то интеграл по С равен интегралу по 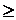 , т.к.
, т.к.
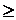 и С функция аналитическая.
и С функция аналитическая. Опр. В ряде Лорана  первая сумма называется правильной частью ряда Лорана, а вторая сумма – главной частью.
первая сумма называется правильной частью ряда Лорана, а вторая сумма – главной частью.
Следствие1. Правильная часть сходится в круге  , а главная часть вне круга радиуса r (т.е. при
, а главная часть вне круга радиуса r (т.е. при  )
)
Следствие2. Из доказательства теоремы вытекает, что ряд Лорана находится единственным образом.
Пример1.




-2 0 2

 ;
;
Первое слагаемое сходится при  , т.е.
, т.е.  , т.е. вне малой окружности.
, т.е. вне малой окружности.
Второе слагаемое сходится при  ,
,  , т.е. внутри большой окружности.
, т.е. внутри большой окружности.
Таким образом получен ряд Лорана в кольце  .
.
 Пример2.
Пример2.
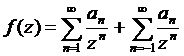
0 2
 ;
;
Первое слагаемое сходится при  .
.
Опр. Ряд в области  называется рядом в окрестности точки
называется рядом в окрестности точки  . Ряд Лорана в окрестности бесконечно удаленной точки.
. Ряд Лорана в окрестности бесконечно удаленной точки.
Утв. Если  - аналитическая в окрестности
- аналитическая в окрестности  -изолированная особая точка, то в окрестности
-изолированная особая точка, то в окрестности  :
:
 .
.
Док-во:
 ,
,
 ;
;