6. Равномерносходящиеся функциональные ряды
-- функциональный ряд, где 
-- функции, заданные на 
Если фиксировать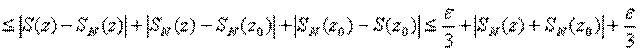 
, то получим 
-- числовой ряд.
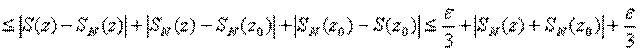-- точка сходимости данного функционального ряда 
-- сумма ряда. Если ряд равномерно сходится, то 
будет непрерывной
1) -- равномерно сходящийся к своей предельной функции на 
, если выполняется следующее условие: 
Теорема6: пусть члены функционального ряда есть функции непрерывные на множестве и данный ряд равномерно сходится на этом множестве, тогда сумма этого ряда есть функция, непрерывная на множестве
Возьмём 
. Тогда:
-- непрерывность функций
-- равномерная сходимость
Так как 
, то она непрерывна как сумма конечного числа непрерывных функций.
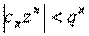
Теорема7 (критерий Коши для равномерной сходимости функциональных рядов): чтобы равномерно сходился на , 
Теорема8 (признак Вейерштрасса)
Пусть 
и 
-- сходится
Тогда равномерно сходится на
Сравнивать комплексные числа мы не можем, поэтому нет признаков Абеля и Дирихле)