Принцип аргумента.
Теорема. Логарифмический вычет функции  относительно контура С равен приращению
относительно контура С равен приращению  аргумента
аргумента  при обходе контура С, деленному на
при обходе контура С, деленному на  , равно разности между числом нулей М и числом полюсов N функции
, равно разности между числом нулей М и числом полюсов N функции  в облости D, ограниченной контуром С:
в облости D, ограниченной контуром С:

 Док-во:
Док-во:
Z W
 |
z w
C
1) 
2) Внутри С  будет иметь конечное число нулей, т.к.
будет иметь конечное число нулей, т.к.
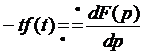
3) 
Теорема Руше.
ЕСЛИ G – односвязная область, С – замкнутый контур, ограничивающий G,  и
и  аналитические в G и на С,
аналитические в G и на С,  на С,
на С,  на С,
на С,  - сумма кратностей всех лежащих в G нулей функции
- сумма кратностей всех лежащих в G нулей функции  ,
,  - сумма кратностей всех лежащих в G нулей функции
- сумма кратностей всех лежащих в G нулей функции  +
+ , ТО
, ТО  .
.
Док-во:
1) 
 2)
2) 
3) 

w
Вектор из начала координат в точку, при такой конфигурации образа С, ни одного оборота не совершит.  .
.
4) 
Пример. Найти количество нулей, которые имеет функция  в круге
в круге  .
.
 ,
,

при  :
: 

 имеет нуль кратности 5
имеет нуль кратности 5  w имеет 5 нулей.
w имеет 5 нулей.
Утв. Если  , то
, то  имеет n корней.
имеет n корней.
Док-во:


С: 
 имеет нуль кратности n, т.о.
имеет нуль кратности n, т.о.
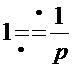 имеет n нулей.
имеет n нулей. Теорема. Если  ,
,  аналитическая в G
аналитическая в G  , то
, то  - аналитическая.
- аналитическая.
Док-во:


1) 



2) аналогично доказываем 
3) Из пунктов 1) и 2) следует, что для F выполнены условия Коши-Римана, следовательно F аналитическая.
Лекция 10