2. Понятие функции комплексной переменного. Предел. Непрерывность
1) Область -- множество точек комплексной плоскости, удовлетворяющих следующим двум условиям:
1) Все точки этого множества внутренние
2) Любые 2 точки этого множества можно соединить ломаной, лежащей в этой области
Область будем обозначать 
 -- область с границей, замкнутая область
-- область с границей, замкнутая область
2) Область  называется односвязной, если она удовлетворяет следующему условию: какую бы замкнутую непрерывную кривую в этой области мы не взяли, часть плоскости, внутренняя по отношению кривой, такжу принадлежит этой области
называется односвязной, если она удовлетворяет следующему условию: какую бы замкнутую непрерывную кривую в этой области мы не взяли, часть плоскости, внутренняя по отношению кривой, такжу принадлежит этой области
Проще говоря, односвязная область -- область без дыр

3) На комплексной плоскости задана функция  , если указано правило, по которому каждому
, если указано правило, по которому каждому  ставится одно или несколько значений
ставится одно или несколько значений  .
.
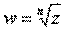 однозначная, во втором -- многозначная
однозначная, во втором -- многозначная  -- однозначная
-- однозначная
 -- многозначная (
-- многозначная ( -значная)
-значная)
Поскольку  , то
, то  ,
,  и
и  -- вещественные функции:
-- вещественные функции: 
4)  , если выполняется условие:
, если выполняется условие: 
5) Функция  называется непрерывной в точке
называется непрерывной в точке  , если
, если  и
и 
Непрерывность в области означает непрерывность в каждой точке области
6)  называется равномерно непрерывной в области
называется равномерно непрерывной в области  , если выполняется следующее условие:
, если выполняется следующее условие: 