3. Понятие аналитической функции. Условия Коши-Римана
1) Производной функции 
в точке 
мы будем называть предел отношения вида: 
2) Функция называется дифференцируемой в точке , если у неё в этой точке существует конечная производная.
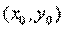
Теорема4 (условие Коши-Римана): пусть 
-- дифференцируема в точке 
, причём 
. Тогда функции 
и 
в точке 
имеют частные производные, причём 
и 
Доказательство: 
1) Пусть 
Тогда 
2) Пусть 
Тогда 
Итак, 
, поэтому и
Данные условия необходимы, но не достаточны
Теорема5: пусть дана
Пусть и -- дифференцируемы в точке , и в этой области выполняется условие Коши-Римана. Тогда -- дифференцируема в точке 
Доказательство:
, 
-- бесконечно малая
, 
-- бесконечно малая
Надо доказать, что существует предел:
3) 
называется дифференцируемой в области, если она дифференцируема в каждой точке этой области
4) Функция называется аналитичной в области 
, если она дифференцируема в области
Понятие аналитичности функции относится к области, но бы и про конкретную точку будем говорить, что функция аналитична в этой точке, имея ввиду аналитичность в окрестности этой точки