19. Первообразная аналитической функции
 -- первообразная
-- первообразная  в области
в области 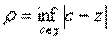 , если
, если 
Любые две первообразные функции отличаются комплексной константой
Теорема14: пусть функция  аналитична в области
аналитична в области 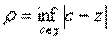 .
.
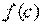 . Тогда
. Тогда 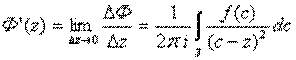 является первообразной
является первообразной 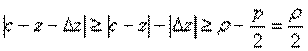 в области
в области 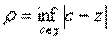 , то есть
, то есть 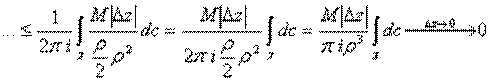
Доказательство: дадим точке  приращение
приращение  , чтобы
, чтобы  . Тогда:
. Тогда:

Тогда 

Итак, 
Надо доказать, что 
Получаем 
Так как 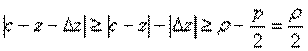 аналитична в
аналитична в 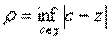 , то
, то 
Поэтому 
Поэтому, очевидно, что 
Перейдя к пределу в равенстве  , получим
, получим

Теорема15 (формула Ньютона-Лейбница):
Пусть 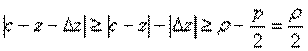 -- аналитична в
-- аналитична в 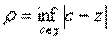
Пусть  -- первообразная
-- первообразная 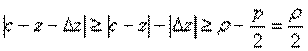 в
в 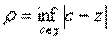
Тогда 
По Т14, 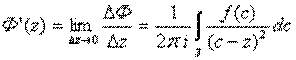 -- первообразная
-- первообразная 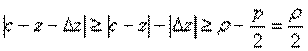 в области
в области 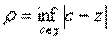 ,
, 
С другой стороны, 
 , поэтому
, поэтому 
Поэтому 
Пример: 
Источник:
Лекции по комплексным числам. 2016
Еще по теме 19. Первообразная аналитической функции:
-
Аналитическая геометрия -
Вариационное исчисление -
Векторный и тензорный анализ -
Высшая геометрия -
Высшая математика -
Вычислительная математика -
Дискретная математика -
Дифференциальное и интегральное исчисление -
Дифференциальные уравнения -
Исследование операций -
История математики -
Комплексное исчисление -
Линейная алгебра -
Линейное программирование -
Математика для экономистов -
Математическая логика -
Математическая физика -
Математический анализ -
Пределы -
Ряды -
Статистика -
Теория вероятностей -
Теория графов -
Теория игр -
Теория принятия решений -
Теория случайных процессов -
Теория чисел -
Функциональный анализ -
-
Архитектура и строительство -
Безопасность жизнедеятельности -
Библиотечное дело -
Бизнес -
Биология -
Военные дисциплины -
География -
Геология -
Демография -
Диссертации России -
Естествознание -
Журналистика и СМИ -
Информатика, вычислительная техника и управление -
Искусствоведение -
История -
Культурология -
Литература -
Маркетинг -
Математика -
Медицина -
Менеджмент -
Педагогика -
Политология -
Право России -
Право України -
Промышленность -
Психология -
Реклама -
Религиоведение -
Социология -
Страхование -
Технические науки -
Учебный процесс -
Физика -
Философия -
Финансы -
Химия -
Художественные науки -
Экология -
Экономика -
Энергетика -
Юриспруденция -
Языкознание -