Операционное исчисление
Опр. Функция  называется оригиналом, если:
называется оригиналом, если:
1) 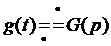 определена при
определена при  ,
, 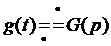 и
и  являются кусочно-непрерывными на любом конечном интервале,
являются кусочно-непрерывными на любом конечном интервале,
2) при 
3) .
.
Утв. Если  -многочлен степени n,
-многочлен степени n,  то
то  .
.
Док-во:
 ,
,  по правилу Лопиталя
по правилу Лопиталя 
 ;
; .
.
Опр.  называется изображением, соответствующим оригиналу f(t), если F(p) – интеграл Лапласа:
называется изображением, соответствующим оригиналу f(t), если F(p) – интеграл Лапласа:
 ;
;  .
.
Теорема.
Если f(t) оригинал, то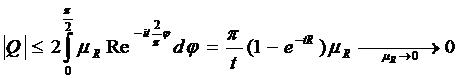 - изображение
- изображение 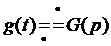 ,
, 1)  сходится в полуплоскости
сходится в полуплоскости  ,
,
2)  является в полуплоскости
является в полуплоскости  аналитической функцией от p.
аналитической функцией от p.
Док-во:
1)


 , таким образом F(p) сходится.
, таким образом F(p) сходится.
2) Аналитичность следует из теоремы, доказанной в предыдущей лекции.
След. Если F(p) – изображение некоторого оригинала, то 
Зам. Если  , то F(p) сходится равномерно.
, то F(p) сходится равномерно.
Еще по теме Операционное исчисление:
-
Аналитическая геометрия -
Вариационное исчисление -
Векторный и тензорный анализ -
Высшая геометрия -
Высшая математика -
Вычислительная математика -
Дискретная математика -
Дифференциальное и интегральное исчисление -
Дифференциальные уравнения -
Исследование операций -
История математики -
Комплексное исчисление -
Линейная алгебра -
Линейное программирование -
Математика для экономистов -
Математическая логика -
Математическая физика -
Математический анализ -
Пределы -
Ряды -
Статистика -
Теория вероятностей -
Теория графов -
Теория игр -
Теория принятия решений -
Теория случайных процессов -
Теория чисел -
Функциональный анализ -
-
Архитектура и строительство -
Безопасность жизнедеятельности -
Библиотечное дело -
Бизнес -
Биология -
Военные дисциплины -
География -
Геология -
Демография -
Диссертации России -
Естествознание -
Журналистика и СМИ -
Информатика, вычислительная техника и управление -
Искусствоведение -
История -
Культурология -
Литература -
Маркетинг -
Математика -
Медицина -
Менеджмент -
Педагогика -
Политология -
Право России -
Право України -
Промышленность -
Психология -
Реклама -
Религиоведение -
Социология -
Страхование -
Технические науки -
Учебный процесс -
Физика -
Философия -
Финансы -
Химия -
Художественные науки -
Экология -
Экономика -
Энергетика -
Юриспруденция -
Языкознание -