25. Нули аналитической функции
1)  называется целой, если она аналитична во всей комплексной плоскости
называется целой, если она аналитична во всей комплексной плоскости
Теорема24 (Лиувилля): если  -- целая и ограниченная, то
-- целая и ограниченная, то  тождественно равна константе
тождественно равна константе
Пусть 
Во всей комплексной плоскости  .
.
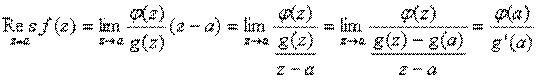
Если  , то
, то  при
при 
Поэтому  (константа)
(константа)
2) Функция  называется голоморфной (регулярной) в точке
называется голоморфной (регулярной) в точке  , если существует окрестность этой точки, в которой функция раскладывается в степенной ряд
, если существует окрестность этой точки, в которой функция раскладывается в степенной ряд
Замечание: понятия голоморфности и аналитичности эквивалентны
3) Нули аналитической функции
Мы будем говорить, что функция  в точке
в точке  -- ноль кратности
-- ноль кратности  , если:
, если:
 ,
,  ,
,  ,...,
,...,  ,
, 
Если  , мы будем говорить, что функция в точке
, мы будем говорить, что функция в точке  имеет простой нуль, или нуль первого порядка
имеет простой нуль, или нуль первого порядка
Очевидно, что если  -- ноль
-- ноль  -го порядка, то разложение Тейлора в окрестности этой точки имеет вид:
-го порядка, то разложение Тейлора в окрестности этой точки имеет вид:  , где
, где 
Теорема25: чтобы функция  имела в точке
имела в точке  нуль
нуль  -го порядка, необходимо и достаточно, чтобы она была представима в виде:
-го порядка, необходимо и достаточно, чтобы она была представима в виде:  , где
, где  , а функция
, а функция  -- аналитична в точке
-- аналитична в точке 
1) Необходимость: пусть  в точке
в точке  имеет нуль
имеет нуль  -го порядка, и значит, разложение в ряд Тейлора имеет вид:
-го порядка, и значит, разложение в ряд Тейлора имеет вид: 

2) Достаточность:  ,
, 
Тогда 
Итак,  ,
,  ,...,
,...,  ,
, 
Поэтому  -- ноль
-- ноль  -го порядка
-го порядка