Логарифм
Логарифмическая функция определяется как функция, обратная экспоненте.
Аргумент экспоненты определён неоднозначно, поэтому логарифмическая функция, в отличие от ранее рассмотренных, является неоднозначной.
Обозначим через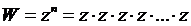
значение логарифма при некотором фиксированном 
. Докажем следующее свойство логарифмической функции:
Доказательство
Представим z в показательной форме:
в точке А 
Будем перемещаться из точки А в точку 
по окружности.
В этом случае 
Если будем дальше двигаться по окружности, то действительная часть будет неизменна, а мнимая будет расти. Сделав полный круг получим:
Логарифм получил приращение 
. Логарифм относится к классу многозначных аналитических функций.
Рассмотрим интеграл: 
.
Точка z=0 – особая точка. Она будет также точкой ветвления. Произведём замену переменных:
Значит, функция 
не имеет особых точек.
Так как при обходе контура L обходится точка ветвления, то прибавляется приращение