Лекция 5 Теорема Коши для многосвязных областей
Пусть область D – двусвязная, иными словами, ее нельзя стянуть в точку за счет деформации граничного контура 
.
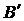содержится область 
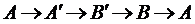, ограниченная контуром Г.
 |
Требуется, как и выше, найти контурный интеграл
Выберем произвольную точку А на L и соединим её с точкой В на Г. По отрезку АВ выполним математический разрез (разрез, не имеющий ширины), как показано на рисунке справа. Точка А совпадает с точкой 
, а В – с 
. Разрезанная таким образом область превращается в односвязную с граничным контуром 
.
Будем двигаться так (вдоль контура): 
. В этом случае разобранная выше теорема Коши дает:
.
.
В общем случае, когда область D есть 
-связная область, то есть содержит внутри себя n областей, получается: 
Теорема Морера
Пусть 
- функция, непрерывная в области D. Если для любого замкнутого непересекающегося контура, целиком лежащего в области D, справедливо равенство 
, то функция 
голоморфна в области D.
Доказательство:
откуда следуют условия Коши-Римана.