Лекция 3 Конформные отображения
 |
Пусть дана функция w=f(z) (иначе w=w(z))
Продифференцируем:
Рассмотрим комплексные числа:
Геометрически это можно изобразить так:
 |
Геометрически это можно изобразить так:
 |
Рассмотрим преобразование вектора dz в dw (
).
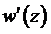имеет модуль R и аргумент 
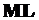. В точке М производная 
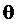имеет модуль r и аргумент 
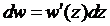. Поэтому в результате конформного отображения вектор 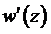поворачивается против часовой стрелки на угол 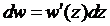, а его модуль увеличивается в r раз. Вектор 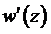был выбран произвольно, но при условии, что он лежит в малой окрестности точки М. Выберем другой вектор 
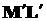, повёрнутый относительно 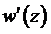на угол 
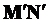. Вектор 
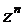является отображением вектора 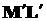и будет повёрнут относительно 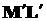на угол 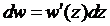против часовой стрелки. Рассмотрим угол между 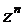и 
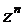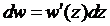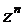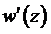. В силу того, что и получились в результате поворота исходных векторов на один угол (), угол между и будет равен углу между исходными векторами и 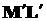, то есть углу .
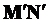Следовательно, при конформном отображении сохраняется угол между векторами.
Геометрический смысл модуля аргумента производной функции комплексного переменного: векторы в точке М растягиваются в r раз, а аргумент поворачивает эти векторы на 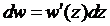радиан против часовой стрелки.
Если в некоторой точке области D функция f(z) непрерывна и имеет непрерывную производную, то функция называется регулярной в этой точке. Если функция f(z) регулярна во всех точках области D, то такая функция называется голоморфной в этой области.