27. Классификация изолированных особых точек. Теорема Сохоцкого
1) Точка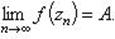 
называется изолированной особой точкой для 
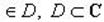, если 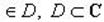аналитична в кольце вида 
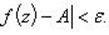(всюду аналитична в окрестности этой точки за исключением самой точки)
Пусть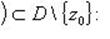 
-- изолированная особая точка функции .
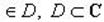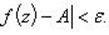, то она допускает разложение в ряд Лорана 2) Точка 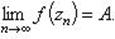называется устранимой особой точкой, если разложение в ряд Лорана не содержит отрицательных степеней: 
. Особенность легко можно устранить, положив 
3) Точка 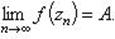называется точкой типа “полюс”, если разложение в ряд Лорана содержит конечное число 
отрицательных степеней. При этом если 
, то 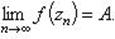-- простой полюс, или полюс первого порядка, а если 
, то полюс кратности или полюс -го порядка
4) Точка 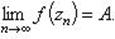-- существенная особая точка для 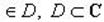, если разложение в ряд Лорана содержит бесконечное число отрицательных степеней
Теорема27: пусть точка 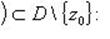-- ноль -го порядка аналитической функции 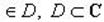, тогда функция 
в точке 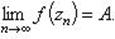имеет полюс -го порядка
Доказательство:
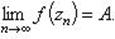-- ноль -го порядка, поэтому 
, где 
аналитична в точке 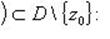и 
Тогда 
Так как 
, то 
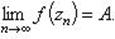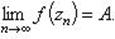аналитична в точке . Поэтому в окрестности точки раскладывается в ряд Тейлора: 
.
Поэтому 
Так как , то 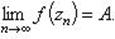-- полюс -го порядка для функции
Теорема28: пусть 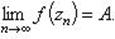-- полюс для 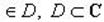. Тогда 
Доказательство: 
Теорема29 (теорема Сохоцкого): пусть точка 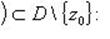-- существенно особая точка функции 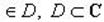. Тогда каково бы ни было
(конечное или бесконечное), существует последовательность 
из области определения функции 
такая, что 
Доказательство:
1) Пусть 
, тогда 
.
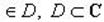была бы ограничена в окрестности 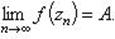, и точка 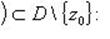являлась бы устранимой 2) Пусть -- число. Предположим, что не существует ни одной такой последовательности