22. Интеграл типа Коши
Пусть 
-- непрерывна на
.
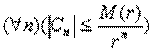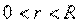. Понятно, что если 
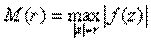, то подынтегральная функция 
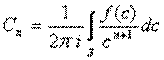-- непрерывна на кривой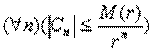 
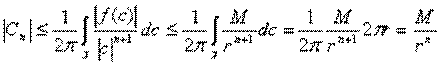
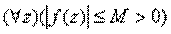-- всегда существует Итак, интеграл Коши, то есть 
Теорема18: интеграл типа Коши есть функция аналитическая в любой точке своей области определения (
. Более того, эта функция является бесконечно дифференцируемой
Итак, 
Докажем, что второе слагаемое 
при 
:
Пусть 
.
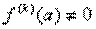
Поскольку 
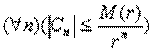-- непрерывно на , то оно ограничено на 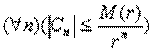, поэтому 
Поэтому 
Поэтому 
Проведя аналогичные выкладки для 
, получаем: 
Далее по индукции можно получить: 
Теорема19: пусть -- аналитична в 
. Тогда она в этой области имеет производные сколь угодно большого порядка
Пусть 
, пусть 
. Тогда по интегральной формуле Коши, 
Значит, у нашей функции в точке 
существует производная. По теореме18, в точке имеет производные сколь угодно большого порядка, причём вычислятся так: 
В силу произвольности выбора точки , это верно для любой точки из области