Интеграл Коши
Рассмотрим некоторую функцию f(z), голоморфную в односвязной области D. На контуре L функция не обязательно голоморфна, но обязательно непрерывна. Она также непрерывно продолжима на контур L из любой внутренней точки области D.
Пусть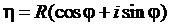
- некоторая внутренняя точка области 
.
 |
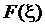При этом справедлива формула 
- формула Коши.
Доказательство:
Рассмотрим функцию 
- голоморфную в области D за исключением точки 
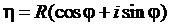с координатой , где она не определена.
Окружим точку М(z) контуром Г. Тогда по теореме Коши для многосвязных областей получим
Так как функция 
голоморфна повсюду, кроме точки z, то контур Г – произвольный. Нужно лишь, чтобы он охватывал точку M и лежал внутри контура 
. В качестве Г возьмём окружность, радиус которой стремится к нулю.
Введём локальную систему координат с центром в точке M. Пусть
. Выполним предельный переход
