Функциональные последовательности и ряды
 Пусть в области D задана последовательность голоморфных функций:
Пусть в области D задана последовательность голоморфных функций:
 .
.
Определение: последовательность сходится равномерно, если для  и некоторого произвольного числа
и некоторого произвольного числа 
 , такое, что
, такое, что 

Функция  называется пределом последовательности:
называется пределом последовательности: 
Теорема[3]
Если функции, из которых составлена равномерно сходящаяся последовательность, непрерывные, то и предел этих функций также является непрерывной функцией.
Теорема
Пусть дана равномерно сходящаяся последовательность функций  , (
, ( ), тогда:
), тогда:

или иначе

Доказательство:
В силу того, что последовательность сходится равномерно, можно выбрать малое  такое, что при n>N будет выполняться условие:
такое, что при n>N будет выполняться условие:  .
.
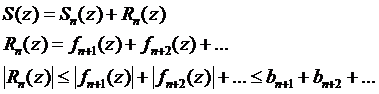 .
. 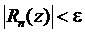
Определение:
 - функциональный ряд.
- функциональный ряд.
Если  , такое что
, такое что  , где
, где  - частичная сумма, то такой функциональный ряд сходится равномерно.
- частичная сумма, то такой функциональный ряд сходится равномерно.
Рассмотрим понятие мажорирующего ряда:
пусть  - сходящийся числовой ряд
- сходящийся числовой ряд  . Тогда, если
. Тогда, если  такое, что:
такое, что:  , то
, то  - мажорирующий ряд, а
- мажорирующий ряд, а  - мажорируемый ряд.
- мажорируемый ряд.
Теорема
Всякий мажорируемый ряд равномерно сходится.
Доказательство:

откуда следует, что  .
.
Теорема
Равномерно сходящийся функциональный ряд можно почленно интегрировать.
Доказательство:


Тогда

Таким образом, доказано, что
