Функции комплексного переменного
Опр. Если даны множества М и G на комплексной плоскости и каждому z из M соответствует w из G, то говорят, что  функция
функция  .
.
Опр. 
 ;
;




Опр. (1)  - степенной ряд.
- степенной ряд.
Утв. Ряд (1) сходится внутри круга  и расходится вне его. При
и расходится вне его. При 
 он сходится равномерно.
он сходится равномерно.
Некоторые разложения:

 ;
;

 ;
;

 ;
;
Докажем формулу Эллера:
 = cos
= cos + i*sin
+ i*sin

 ;
;
 ;
;
 -доказывается умножением рядов.
-доказывается умножением рядов.
 ;
;
 ;
;
Периодичность функции  :
:
 ;
;
Опр.
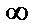 =
=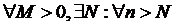 , если
, если 


Опр. Множество точек z:  называется окрестностью бесконечно удаленной точки.
называется окрестностью бесконечно удаленной точки.
Лекция 2
Еще по теме Функции комплексного переменного:
-
Аналитическая геометрия -
Вариационное исчисление -
Векторный и тензорный анализ -
Высшая геометрия -
Высшая математика -
Вычислительная математика -
Дискретная математика -
Дифференциальное и интегральное исчисление -
Дифференциальные уравнения -
Исследование операций -
История математики -
Комплексное исчисление -
Линейная алгебра -
Линейное программирование -
Математика для экономистов -
Математическая логика -
Математическая физика -
Математический анализ -
Пределы -
Ряды -
Статистика -
Теория вероятностей -
Теория графов -
Теория игр -
Теория принятия решений -
Теория случайных процессов -
Теория чисел -
Функциональный анализ -
-
Архитектура и строительство -
Безопасность жизнедеятельности -
Библиотечное дело -
Бизнес -
Биология -
Военные дисциплины -
География -
Геология -
Демография -
Диссертации России -
Естествознание -
Журналистика и СМИ -
Информатика, вычислительная техника и управление -
Искусствоведение -
История -
Культурология -
Литература -
Маркетинг -
Математика -
Медицина -
Менеджмент -
Педагогика -
Политология -
Право России -
Право України -
Промышленность -
Психология -
Реклама -
Религиоведение -
Социология -
Страхование -
Технические науки -
Учебный процесс -
Физика -
Философия -
Финансы -
Химия -
Художественные науки -
Экология -
Экономика -
Энергетика -
Юриспруденция -
Языкознание -