Дифференцирование функций комплексной переменной
Производная функции комплексной переменной определяется следующим образом:


Будем считать, что функции  и
и  регулярны в области
регулярны в области  : непрерывны и имеют непрерывные частные производные по аргументам
: непрерывны и имеют непрерывные частные производные по аргументам  и
и  .
.
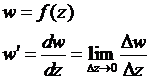 должна быть функцией только одного комплексного аргумента -
должна быть функцией только одного комплексного аргумента - 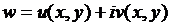 . Выше было показано, что комплексная функция, построенная из двух функций двух действительных переменных
. Выше было показано, что комплексная функция, построенная из двух функций двух действительных переменных 
при переходе к комплексным аргументам записывается в виде  . Чтобы выполнялось соотношение
. Чтобы выполнялось соотношение  , необходимо и достаточно выполнения условия
, необходимо и достаточно выполнения условия

Получим
 Полученные равенства называются условиями Коши-Римана.
Полученные равенства называются условиями Коши-Римана.
Предположим теперь, что функции  дважды дифференцируемы в области
дважды дифференцируемы в области  .
.
Исключим v из соотношений Коши-Римана:

Исключим теперь u:

Таким образом, функции  удовлетворяют уравнению Лапласа и, следовательно, они являются гармоническими функциями.
удовлетворяют уравнению Лапласа и, следовательно, они являются гармоническими функциями.
Еще по теме Дифференцирование функций комплексной переменной:
-
Аналитическая геометрия -
Вариационное исчисление -
Векторный и тензорный анализ -
Высшая геометрия -
Высшая математика -
Вычислительная математика -
Дискретная математика -
Дифференциальное и интегральное исчисление -
Дифференциальные уравнения -
Исследование операций -
История математики -
Комплексное исчисление -
Линейная алгебра -
Линейное программирование -
Математика для экономистов -
Математическая логика -
Математическая физика -
Математический анализ -
Пределы -
Ряды -
Статистика -
Теория вероятностей -
Теория графов -
Теория игр -
Теория принятия решений -
Теория случайных процессов -
Теория чисел -
Функциональный анализ -
-
Архитектура и строительство -
Безопасность жизнедеятельности -
Библиотечное дело -
Бизнес -
Биология -
Военные дисциплины -
География -
Геология -
Демография -
Диссертации России -
Естествознание -
Журналистика и СМИ -
Информатика, вычислительная техника и управление -
Искусствоведение -
История -
Культурология -
Литература -
Маркетинг -
Математика -
Медицина -
Менеджмент -
Педагогика -
Политология -
Право России -
Право України -
Промышленность -
Психология -
Реклама -
Религиоведение -
Социология -
Страхование -
Технические науки -
Учебный процесс -
Физика -
Философия -
Финансы -
Химия -
Художественные науки -
Экология -
Экономика -
Энергетика -
Юриспруденция -
Языкознание -