Аналитическое продолжение
Пусть в односвязной области 
задана функция 
, а в односвязной области 
.
Если можно ввести такую функцию, то говорят, что 
является аналитическим продолжением функции в области 
и наоборот.
Достаточный признак существования аналитического продолжения:
Пусть 
- граница раздела и . Пусть функции 
и 
непрерывны на границе . Кроме того, пусть на границе выполнено условие 
; в этом случае существует аналитическое продолжение.
Доказательство:
Если внутри D для любого контура L выполнено условие 
, то внутри D функция f(z) аналитическая (теорема Морера).
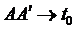. Если выберем в 
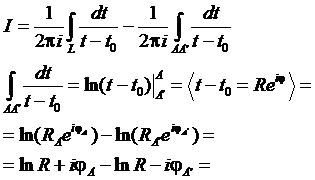. Рассмотрим следующий контур L:
- если это равенство верно, то справедливо 
и, следовательно (теорема Морера), функция 
- аналитическая в области D.
Рассмотрим контур 
.
+
=0
Рассмотрим контур 
.
Складывая эти два равенства, получим: .