1. Сходящиеся последовательности в метрических пространствах и полные метрические пространства
В метрическом пространстве вводится понятие сходимости последовательности. Пусть (Х, d) – метрическое пространство.
Определение 1. Говорят, что xnÎХ сходится к xÎХ (xn ® x; 
), если d(xn, x) ® 0 при n ® ¥.
Понятие сходимости можно сформулировать и на языке «e-n». Для " e > 0 $ n0(e): для " n ? n0 справедливо неравенство d(xn, x) < e.
Лемма 1. Если последовательность в метрическом пространстве сходится, то ее предел единственный.
Доказательство. Пусть хn ® а, хn ® b. Применяя неравенство треугольника, получим: d(а, b) £ d(а, хn) + d(хn, b). Оба слагаемых в правой части стремятся к нулю. Так как d(а,b) неотрицательное и не зависит от n, то по известным теоремам о переходе к пределу в неравенствах получаем d(а,b) = 0, а тогда по свойствам метрики а = b, что и требовалось доказать.
Определение 2. Последовательность хn элементов метрического пространства Х называется ограниченной, если существует шар S(y, r), которому принадлежат все члены последовательности.
Лемма 2. Если последовательность сходится в метрическом пространстве, то она ограничена.
Доказательство. Утверждение легко вытекает из определения сходящейся последовательности, если заметить, что если хn ® х, то для " фиксированного e > 0 найдется n0, для которого xnÎS(x, e) для всех n ? n0. Следовательно, все члены последовательности за исключением конечного числа попадают в окрестность S(x, e). Так как любой конечный набор элементов является всегда ограниченным, отсюда уже следует ограниченность всей последовательности.
Следствие. Если последовательность {xn} точек из X сходится к точке xÎX, то числа d(xn, y) ограничены для любой фиксированной точки у пространства X.
Лемма 3. Если xn → x, yn→ y, то d(xn, yn) → d(x, y) (иначе говоря, метрика является непрерывной функцией своих аргументов).
Доказательство. По неравенству четырёхугольника
|d(x, y) - d(xn, yn)| 
d(x, xn) + d(y, yn).
Отсюда предельным переходом при n → 
легко получаем утверждение леммы.
В метрическом пространстве предельными для множества являются такие точки х0, для которых существует последовательность точек хn множества сходящаяся к х0. Замкнутый шар S[a, r] есть замкнутое множество. В самом деле, пусть xn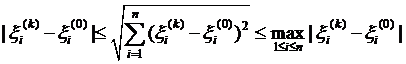 
S[a, r] и xn → x0. Тогда d(xn, a) r, и при n → это неравенство в пределе дает d(x0, a) r, т.е. х0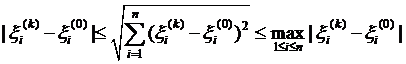S[a, r]. А так как каждая предельная точка шара есть предел некоторой последовательности точек шара, то замкнутость шара доказана.
Выясним конкретный смысл сходимости в метрических пространствах Rn, C[a, b], l2 и m.
Пример 1. Пусть Х = Rn. Если хк→х0, где хк ={ξ1(к),…, ξn(к) } и х0 ={ξ1(0),…, ξn(0) }, то
d(хк, х0) = 
→0 при к → ∞.
Но в силу несложно проверяемых неравенств
,
верных для любого i, это возможно тогда и только тогда, когда ξi(k) → ξi(0), i = 1,..., n, при k → ∞.
Отсюда следует, что сходимость в Rn есть сходимость координат точек последовательности к соответствующим координатам точки – предела, т.е. сходимость в Rn есть сходимость по координатам.
Пример 2. Пусть Х = C[a, b]. Если {xn(t)} 
C[a, b] сходится к х0(t) 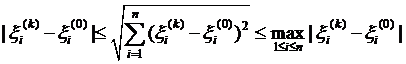C[a, b], то
d(хn, х0) = 
|xn(t) – x0(t)| → 0
или иначе: 
ε >0 
N: n > N => |xn(t) – x0(t)|< ε. Это условие эквивалентно условию, что n > N => |xn(t) – x0(t)|< ε t 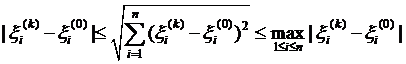[a, b]. Но это означает равномерную сходимость последовательности {xn(t)} к х0(t). Таким образом, сходимость в пространстве С[a, b] есть равномерная сходимость функциональной последовательности {xn(t)}.
Пример 3.
Пусть Х = l2. Можно показать ,что сходимость последовательности {xn}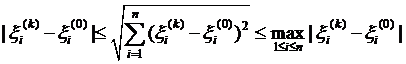 l2 к х0 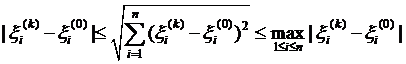l2, где хn ={ξi(n) }, х0 ={ξi(0) } означает, что 1) ξi(n) → ξi(0) для i = 1,2,...
2) ε>0 N: 
0 N: " n > N ? | ξi(n) – ξi(0) | 0 $ N: d(xn, xm) < e, если n, m ?N.
Лемма 4 (о сходимости последовательностей). Пусть {xn} – последовательность из метрического пространства Х. Следующие условия эквивалентны:
1. {xn} – сходится к х;
2. Любая подпоследовательность {xn} сходится х;
3. Для любой подпоследовательности {
} существует подпоследовательность {
} сходящаяся к х;
4. {xn} – фундаментальная и любая подпоследовательность {} сходится к х;
5. {xn} – фундаментальная и существует подпоследовательность {}, сходящаяся к х.
Доказательство.
1. ? 2. и 2. ? 3. Стандартные утверждения из математического анализа: подпоследовательность сходящейся последовательности сходится к тому же пределу: доказательство абсолютно аналогично.
4. ? 5. Очевидно.
3. ? 4. вытекает из 5. ? 1. Действительно, если 5. ? 1. уже доказано, то в силу условий п.4. подпоследовательность {} фундаментальна, но по п. 3 у нее существует сходящаяся к х подпоследовательность. Тогда из 5. ? 1. вытекает, что {} сама сходится к х.
5. ? 1. Пусть {xn} – фундаментальная последовательность и 
– ее сходящаяся к х подпоследовательность. Для " e > 0 $ N1: d(xp, xm) < e, p, m > N1. Полагая здесь m = nk, nk ? N1, k ? N, имеем d(xp, 
) < e. Следовательно, d(x, xp) £ d(x, ) + d(, xp) £ e+e £ 2e (p > N1) и xp ® x Î Х.
Определение 4. Метрическое пространство Х называется полным, если любая фундаментальная последовательность в этом пространстве сходится к элементу этого пространства.
Пример 5. Для случая Rn – евклидова n–мерного пространства – полнота следует из критерия Коши существования предела последовательности точек этого пространства.
Пример 6. Рассмотрим введенное выше пространство С[0, 1]. По определению фундаментальной последовательности {xn} и метрики для " e>0 $N: 
< e "n, m ? N. Если мы зафиксируем t, то хn(t) будет обычной числовой фундаментальной последовательностью, у которой существует в силу критерия Коши поточечный предел х(t). Переходя к поточечному пределу в неравенстве 
верном для любого t Î [0, 1] при m ® ¥ получаем 
£ e для " n ? N.
Пример 7. На множестве C[0, 1] можно ввести другую метрику, например:
d(x, y) = 
но в этом случае пространство не будет полным. Для доказательства этого достаточно рассмотреть следующую последовательность непрерывных функций:
хn(t) = 
Покажите, что эта последовательность фундаментальна по приведенной метрике (используйте геометрический смысл определенного интеграла), но сходится к разрывной функции.
Пример 8. Покажем полноту пространства l2. Пусть последовательность х(m) = (x1(m), x2(m),..., xn(m),....), m = 1, 2, .... является фундаментальной в l2. Следовательно, для произвольно выбранного e > 0 существует такой номер n0, что для всех k, m ? n0 выполняется неравенство 
< e. Из неравенства |xn(m) - xn(k)| £ , верного для любого n Î N, вытекает фундаментальность последовательности {xn(m)} в пространстве R и следовательно ее сходимость xn(m) ® хn при m ®¥. Переходя в очевидном неравенстве
< e
при фиксированном m к пределу сперва при k ®¥, затем при p ®¥, получим неравенство
£ e.
Из неравенства треугольника
вытекает принадлежность х к l2. Из предыдущего же неравенства вытекает сходимость х(m) к х в l2.