5. Ряды Фурье в гильбертовом пространстве. Коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля. Полные и замкнутые ортонормированные системы
Пусть L – подпространство гильбертового пространства Н, порожденное ортонормальной системой  и
и  .
.
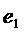 существует, линейная комбинация
существует, линейная комбинация 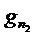 , такая, что
, такая, что 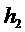 . Но
. Но 
 , где
, где  .
.
Числа сi называются коэффициентами Фурье вектора x относительно ортонормальной системы 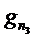 . Из последнего равенства получаем
. Из последнего равенства получаем
 .
.
Отсюда следует, что норма разности  принимает наименьшее значение, когда коэффициенты
принимает наименьшее значение, когда коэффициенты  являются коэффициентами Фурье элемента
являются коэффициентами Фурье элемента  относительно системы
относительно системы 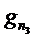 . В этом случае имеем
. В этом случае имеем
 , (7)
, (7)
и так как  можно выбрать сколь угодно малым, то
можно выбрать сколь угодно малым, то

Из формулы (7) следует также, что ряд  сходится причём
сходится причём  .
.
Пусть теперь x – любой элемент пространства H. Обозначим через z проекцию x на L; тогда  , где
, где  и
и  . Так как
. Так как  ,
,  ,
,  , то
, то  . Следовательно, для любого элемента x из H справедливо неравенство
. Следовательно, для любого элемента x из H справедливо неравенство
 ,
,
где  ,
,  . Это соотношение называется неравенством Бесселя.
. Это соотношение называется неравенством Бесселя.
Пусть в пространстве H дана ортонормальная система элементов 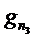 . Если не существует элемента
. Если не существует элемента  , отличного от нулевого и ортогонального всем элементам системы
, отличного от нулевого и ортогонального всем элементам системы 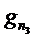 , то эта система называется полной. Ортонормальная система
, то эта система называется полной. Ортонормальная система 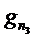 называется замкнутой, если подпространство L, порождаемое этой системой, совпадает с H. Ряд Фурье по замкнутой системе, построенной для любого
называется замкнутой, если подпространство L, порождаемое этой системой, совпадает с H. Ряд Фурье по замкнутой системе, построенной для любого  , сходится к этому элементу и для любого
, сходится к этому элементу и для любого  имеет место равенство Парсеваля
имеет место равенство Парсеваля

Замкнутая ортонормальная система называется также ортонормальным базисом гильбертова пространства.
Если ортонормальная система полная, то она замкнутая. Поскольку, в этом случае не существует вектора отличного от нулевого и ортогонального линейному многообразию L, порождаемому системой. Но тогда в силу теоремы 9  и система замкнутая.
и система замкнутая.
Обратно, замкнутая ортонормальная система  полна, так как для такой системы
полна, так как для такой системы

и если  ,
,  т.е.
т.е.  ,
,  то
то  , что означает полноту системы
, что означает полноту системы 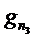 .
.
Примером полной ортонормальной системы является система тригонометрических функций

в пространстве  .
.
Теорема 10. В любом сепарабельном гильбертовом пространстве существует полная ортонормальная система векторов.
Доказательство. Пусть  – любое счётное всюду плотное множество в пространстве H, причём все
– любое счётное всюду плотное множество в пространстве H, причём все  ,
,  отличны от нулевого вектора. Полагаем
отличны от нулевого вектора. Полагаем
 ,
,
и пусть 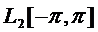 - одномерное пространство, порождённое элементом
- одномерное пространство, порождённое элементом  .
.
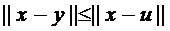 – первый элемент множества G, не принадлежащий
– первый элемент множества G, не принадлежащий 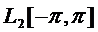 и
и 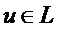 - проекция
- проекция 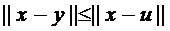 на
на 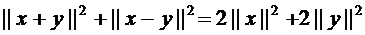 . Полагаем
. Полагаем  .
.
Пусть  - подпространство, порождённое элементами
- подпространство, порождённое элементами  и
и  , и
, и  - первый элемент множества G не принадлежащий
- первый элемент множества G не принадлежащий  . Пусть
. Пусть  - проекция
- проекция  на
на  . Полагаем
. Полагаем
 ,
,
и т.д. Получаем ортонормальную систему  и так как каждый элемент
и так как каждый элемент  принадлежит некоторому
принадлежит некоторому  в силу построения этих подпространств, то подпространство, определяемое системой
в силу построения этих подпространств, то подпространство, определяемое системой 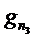 совпадает с подпространством определяемой системой
совпадает с подпространством определяемой системой  , т.е.
, т.е.
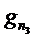 , очевидно счётная, в случае когда, H бесконечномерно, ибо если бы она содержала конечное число p векторов, то в H не существовало бы p + 1 линейно независимых векторов, что противоречит бесконечномерности H. Теорема доказана.
, очевидно счётная, в случае когда, H бесконечномерно, ибо если бы она содержала конечное число p векторов, то в H не существовало бы p + 1 линейно независимых векторов, что противоречит бесконечномерности H. Теорема доказана. Задачи
1. Множество  в линейном пространстве
в линейном пространстве  называется выпуклым множеством, если оно вместе с любым двумя точками
называется выпуклым множеством, если оно вместе с любым двумя точками  содержит все точки
содержит все точки
 ,
,  ,
,  ,
,  ,
,
или, геометрически выражаясь, содержит отрезок, концами которого являются точки  и
и  . Доказать, что любой шар в линейном нормированном пространстве является выпуклым множеством.
. Доказать, что любой шар в линейном нормированном пространстве является выпуклым множеством.
2. Доказать, что неравенство треугольника в определении линейного нормированного пространства можно заменить условием выпуклости единичного шара.
3. На плоскости взято произвольное центрально-симметричное замкнутое выпуклое множество Q, у которого начало координат является внутренней точкой. Доказать, что существует норма, в которой Q является единичным шаром.
4. Доказать, что конечномерное подпространство нормированного пространства Е всегда замкнуто в Е.
5. Задает ли норму в пространстве R1 функция j(х) = |arctgx|?
6. Установить непосредственно эквивалентность следующих норм в  - мерном линейном нормированном пространстве X:
- мерном линейном нормированном пространстве X:
 ,
,
 .
.
Что будут представлять собой единичные шары  и
и  в пространстве
в пространстве  с этими нормами.
с этими нормами.
7. Проверить аксиомы нормированного пространства для пространства матриц  размера
размера  :
:
а)  , б)
, б)  , в)
, в)  .
.
8. Доказать, что пространство  банахово в нормах предыдущего примера.
банахово в нормах предыдущего примера.
9. Доказать, что  ?
?  (Использовать неравенство Минковского).
(Использовать неравенство Минковского).
10. Является ли нормой в пространстве непрерывно-дифференцируе-мых функций C1[a, b] на отрезке [a, b] следующие величины:
a) 
b) |x(b) – x(a)| +
c) |x(a)| +
d) 
11. В множестве непрерывных функций, определённых на  , каждая из которых равна нулю вне некоторого конечного интервала (своего для каждой функции), вводится норма
, каждая из которых равна нулю вне некоторого конечного интервала (своего для каждой функции), вводится норма  . Будет ли пространство этих функций полно в метрике
. Будет ли пространство этих функций полно в метрике  ? Если нет, то что будет пополнением этого пространства?
? Если нет, то что будет пополнением этого пространства?
12. Является ли пространство C1[a, b] банаховым по норме
 .
.
13. Доказать, что пространство M[a, b] – ограниченных на отрезке [a, b] функций с нормой  является банаховым.
является банаховым.
10. Найти бесконечномерное линейное подпространство L Ì  такое, что
такое, что 
11. Показать, что проекция  вектора
вектора  из гильбертова пространства H на подпространство
из гильбертова пространства H на подпространство  есть элемент этого подпространства, находящийся на кратчайшем расстоянии от х, т.е.
есть элемент этого подпространства, находящийся на кратчайшем расстоянии от х, т.е.
 для любого
для любого  .
.
12. Известно, что в некотором нормированном пространстве Е для любой пары векторов х и у справедлива лемма о параллелограмме (т. е.  ). Рассмотрим функцию
). Рассмотрим функцию
 .
.
Доказать, что она удовлетворяет всем аксиомам скалярного произведения и  .
.
13. В гильбертовом пространстве даны последовательности {xn},{yn} такие, что ||xn|| £ 1, ||yn|| £ 1 и (xn, yn)®1. Докажите, что ||xn - yn|| ® 0.
14. Докажите, что множество {x: ||x - a|| = ||x - b||} является выпуклым в гильбертовом пространстве. Верно ли это заключение для произвольного банахова пространства?
15. Пусть в банаховом пространстве Х множества А замкнутое, а B компактное. Докажите, что множество А+B замкнутое. При этом из замкнутости А и B не следует замкнутость А+B.
16. Докажите, что любое семейство замкнутых ограниченных выпуклых множеств в гильбертовом пространстве имеет непустое пересечение. Верно ли это для любого банахова пространства?
17. Пусть аÎ[0, 1] и Сa={xÎС: x(а) = 0}. Докажите, что Сa подпространство С. Является ли оно всюду плотным? А если это множество рассматривать в пространстве L2?
18. Докажите, что множество функций из С, для которых  , является бесконечномерным подпространством в С.
, является бесконечномерным подпространством в С.
19. Пусть В1 и В2 – шары в нормированном пространстве с радиусами соответственно r1 и r2. Доказать, что если В1 Ì В2, то r1 £ r2.