Примеры метрических пространств.
1. Множество вещественных чисел R.
r(х,у) =÷х-у÷. 1 и 2 свойства расстояния очевидны, неравенство треугольника следует из известного неравенства÷а+b÷ £÷a÷+÷b÷ при заменах a: = х-z, b: = z-y.
Сходимость, естественно, совпадает с известным понятием сходимости числовой последовательности.2. Конечномерные метрические пространства  .
.
Рассмотрим множество векторов вида х = (х1,х2,…, хn) c вещественными компонентами. р?1. Определим величину rp(х,у) =  . 1 и 2 свойства метрики очевидны, неравенство треугольника следует из неравенства Минковского (п. 2). Множество n – мерных векторов с расстоянием rp(х,у) является метрическим пространством, которое обозначается
. 1 и 2 свойства метрики очевидны, неравенство треугольника следует из неравенства Минковского (п. 2). Множество n – мерных векторов с расстоянием rp(х,у) является метрическим пространством, которое обозначается  . Cходимость в пространствах
. Cходимость в пространствах  равносильна покоординатной сходимости.
равносильна покоординатной сходимости.
На множестве n-мерных векторов можно определить еще одно расстояние: r¥(х,у) =  . Свойства метрики легко проверяются, впрочем, сходные рассуждения будут приведены в дальнейшем. Здесь сходимость также равносильна покоординатной.
. Свойства метрики легко проверяются, впрочем, сходные рассуждения будут приведены в дальнейшем. Здесь сходимость также равносильна покоординатной.
Пространство  называется эвклидовым.
называется эвклидовым.
Рассмотрим замкнутые шары пространств  при различных значениях р с центром в точке 0 = (0,0) и радиусом 1. Это есть множества вида {(x1,x2):u x1up+ux2up £ 1}.
при различных значениях р с центром в точке 0 = (0,0) и радиусом 1. Это есть множества вида {(x1,x2):u x1up+ux2up £ 1}.
3. Пространство непрерывных функций С.
Рассмотрим множество непрерывных функций, определенных на отрезке [0,1]. Тем самым, здесь точкой является функция. Определим расстояние следующим образом: r(х,у) = . Поскольку функция
. Поскольку функция  непрерывна на отрезке [0,1], то по теореме Вейерштрасса (см. мат. анал!) она достигает максимального значения, так что определение корректно.
непрерывна на отрезке [0,1], то по теореме Вейерштрасса (см. мат. анал!) она достигает максимального значения, так что определение корректно.
Опишем сходимость в этом пространстве. Если хn®x0 в пространстве С[0,1], то  , т.е. "e>0 $N "n>N "tÎ[0,1]
, т.е. "e>0 $N "n>N "tÎ[0,1]  . В математическом анализе такая сходимость функций назывался равномерной в отличие от поточечной, которая состоит в том, что хn(t)®x0(t) при любом tÎ[0,1], т.е. в формальном виде "tÎ[0,1] "e>0 $N "n> N
. В математическом анализе такая сходимость функций назывался равномерной в отличие от поточечной, которая состоит в том, что хn(t)®x0(t) при любом tÎ[0,1], т.е. в формальном виде "tÎ[0,1] "e>0 $N "n> N  .
.
4. Пространство ограниченных последовательностей т.
Рассмотрим множество последовательностей х=(х1,х2,…,хn,…), каждая из которых ограничена, т.е uхnu £М(х) (этим подчеркнуто, что для каждой последовательности границы свои). Например, последовательность (1000, -1, 1000, -1, 1000, -1, 1000,…) входит в т, а последовательность (1, -1, 2, -1, 3, -1, 4,…) нет. Определим расстояние: r(х,у)= Из ограниченности последовательностей х,у следует, что ограничена и последовательность
Из ограниченности последовательностей х,у следует, что ограничена и последовательность  , т.е.
, т.е.
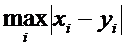 не существует, r(х,у)=1.
не существует, r(х,у)=1. Пусть х(k)®х(0) в пространстве т. Поскольку при любом i  =r(х(k) ,х(0))®0, то в силу неотрицательности по теореме о милиционерах
=r(х(k) ,х(0))®0, то в силу неотрицательности по теореме о милиционерах  ®0, т.е. из сходимости в пространстве т следует покомпонентная сходимость. Обратное неверно: из покомпонентной сходимости не следует сходимость в пространстве т. В качестве примера рассмотрим последовательности х(k), где все компоненты кроме k-ой нулевые, а
®0, т.е. из сходимости в пространстве т следует покомпонентная сходимость. Обратное неверно: из покомпонентной сходимости не следует сходимость в пространстве т. В качестве примера рассмотрим последовательности х(k), где все компоненты кроме k-ой нулевые, а  . Очевидно, что
. Очевидно, что  ®0 при любом i (в соответствующей последовательности все элементы кроме одного нули). В то же время, неверно, что х(k)®0=(0,0,…,0,…), поскольку r(х(k),0) = 1 при всех k. Здесь ситуация аналогична предыдущему примеру: для сходимости в пространстве т нужна не просто покомпонентная сходимость, а равномерная покомпонентная сходимость.
®0 при любом i (в соответствующей последовательности все элементы кроме одного нули). В то же время, неверно, что х(k)®0=(0,0,…,0,…), поскольку r(х(k),0) = 1 при всех k. Здесь ситуация аналогична предыдущему примеру: для сходимости в пространстве т нужна не просто покомпонентная сходимость, а равномерная покомпонентная сходимость.
5. Пространство сходящихся последовательностей с.
Элементами этого пространства являются сходящиеся последовательности х = (х1,х2,…,хn,…) с расстоянием r(х,у) =  . Поскольку сходящиеся последовательности ограничены, пространство с является подпространством пространства т.
. Поскольку сходящиеся последовательности ограничены, пространство с является подпространством пространства т.
6. Пространства непрерывных функций Lpс.
Рассмотрим (аналогично примеру 3) множество непрерывных функций, определенных на отрезке [0,1]. Расстояние между функциями определим формулой rp(х,у)= , где р?1. Свойства расстояния следуют из свойств интеграла и неравенства Минковского. Сходимость может быть весьма экзотичной. Приведем пример последовательности непрерывных функций, которая в Lpс сходится к 0 и при этом не сходится ни в одной точке интервала (0,1). Разобьем отрезок [0,1] на 3 равные части и обозначим через f1(x) функцию, равную 0 в точках 0 и 1, равную 1 на отрезке [1/3, 2/3] и линейную на отрезках [0,1/3] и [2/3,1]. Затем разобьем отрезок на 4 равные части и обозначим через f2(x) функцию, равную 0 на отрезке [3/4,1] и в точке 0, равную 1 на отрезке [1/4,1/2], линейную на отрезках [0,1/4] и [1/2,3/4] и через f3(x) функцию, равную 0 на отрезке [0,1/4] и в точке 1, равную 1 на отрезке [1/2,3/4], линейную на отрезках [1/4,1/2] и [3/4,1]. Рекомендуется сделать рисунок. Продолжим подобное построение. При разбиении отрезка на п частей получим п – 2 новые функции, каждая из которых равна 1 на одном из внутренних промежутков, равна 0 на промежутках, с ним несмежных и линейная на смежных. Построенная последовательность обладает нужными странными свойствами (при любом p), в чем следует убедиться самостоятельно.
, где р?1. Свойства расстояния следуют из свойств интеграла и неравенства Минковского. Сходимость может быть весьма экзотичной. Приведем пример последовательности непрерывных функций, которая в Lpс сходится к 0 и при этом не сходится ни в одной точке интервала (0,1). Разобьем отрезок [0,1] на 3 равные части и обозначим через f1(x) функцию, равную 0 в точках 0 и 1, равную 1 на отрезке [1/3, 2/3] и линейную на отрезках [0,1/3] и [2/3,1]. Затем разобьем отрезок на 4 равные части и обозначим через f2(x) функцию, равную 0 на отрезке [3/4,1] и в точке 0, равную 1 на отрезке [1/4,1/2], линейную на отрезках [0,1/4] и [1/2,3/4] и через f3(x) функцию, равную 0 на отрезке [0,1/4] и в точке 1, равную 1 на отрезке [1/2,3/4], линейную на отрезках [1/4,1/2] и [3/4,1]. Рекомендуется сделать рисунок. Продолжим подобное построение. При разбиении отрезка на п частей получим п – 2 новые функции, каждая из которых равна 1 на одном из внутренних промежутков, равна 0 на промежутках, с ним несмежных и линейная на смежных. Построенная последовательность обладает нужными странными свойствами (при любом p), в чем следует убедиться самостоятельно.
7. Пространства последовательностей lp.
Элементами этого пространства являются последовательности х=(х1,х2,…,хn,…) такие, что ряд  сходится. Например, как следует из курса математического анализа,
сходится. Например, как следует из курса математического анализа,  , но в то же время
, но в то же время  . Расстояние в lp определяется по формуле
. Расстояние в lp определяется по формуле
rр(x,y)= .
.
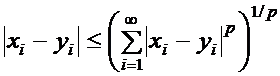 = rр(x,y), то из сходимости в lp следует, что каждая компонента последовательностей сходится, т.е. из х(n)®х(0) следует, что
= rр(x,y), то из сходимости в lp следует, что каждая компонента последовательностей сходится, т.е. из х(n)®х(0) следует, что 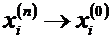 при любом i. Обратное неверно - подходит пример, приведенный для пространства т.
при любом i. Обратное неверно - подходит пример, приведенный для пространства т. 7. Дискретные метрические пространства.
Рассмотрим произвольное множество и определим на нем расстояние таким образом, что r(x,y)=1, если x?y. В этом пространстве шар В(х, e) = В(х,1) (1 > e > 0) содержит только центр шара. Отсюда следует, что последовательность хn сходится тогда и только тогда, когда начиная с некоторого номера ее члены совпадают.
1.