2.2 Оценка риска актива

В качестве численного показателя риска актива могут использоваться следующие показатели:

• ожидаемая доходность;

• стандартное отклонение;

• коэффициент вариации.

Ожидаемую доходность (г) по каждому активу, являющуюся одной из важнейших характеристик эффективности инвестиций.

(2.1)

Где Г; - один из возможных исходов,

Pi - вероятность наступления исхода і,

і - общее число возможных исходов.

То есть ожидаемая доходность актива рассчитывается как, средневзвешенная доходностей при разных будущих состояниях экономики по вероятности наступления этих будущих состояний. Очевидно, что наиболее предпочтительные проекты обладают наибольшей ожидаемой доходностью. Рассчитанная таким образом ожидаемая доходность не является той величиной, которая будет достигнута. Эта величина может рассматриваться как наиболее вероятная или как математическое ожидание доходностей при различных будущих состояниях экономики.

Стандартное отклонение (сг) или корень из дисперсии рассчитывается по следующей формуле:

Данная характеристика является наиболее распространенной для численной оценки риска. Очень часто стандартное отклонение и называют риском (почти всегда при финансовых инвестициях). Отметим, что данный показатель позволяет оценить отклонения величин доходности от ожидаемого значения. Соответственно, чем меньше разброс значений доходности при различных состояниях экономики, тем меньшим уровнем риска будет характеризоваться данный актив. Необходимо понимать, что использование стандартного отклонения или дисперсии как меры риска предполагает нормальное распределение доходности, иными словами, значения доходностей актива при разных состояниях экономики должны быть симметричны относительно ожидаемой доходности.

Известно, что уровень риска и величина доходности в большинстве случаев находятся в прямой зависимости, т. е. увеличение доходности возможно при соответствующем увеличений риска активы, и наоборот. Но мера риска является величиной условной и относительной, поэтому может так оказаться, что некоторые проекты обладают одинаковым риском, рассчитанным по одному из двух предложенных методов. В этом случае для оценки риска используется показатель коэффициента вариаций (Var), который рассчитывается как отношение стандартного отклонения к ожидаемой доходности:

/

Из нескольких альтернативных активов, предпочтение отдается тому активу, который имеет наименьший коэффициент вариации, т.е. имеет наименьший уровень риска на единицу доходности.[23]

Задача 2.1. Рассчитать показатели риска активов А и В, если известна следующая информация:

			2.3 Анализ портфельного риска В качестве численного показателя портфельного риска используются следующие показатели: • ожидаемая доходность портфеля; • стандартное отклонение портфеля; • коэффициент вариации портфеля. Ожидаемая доходность портфеля ценных бумаг (Jp) - это просто средневзвешенное значение ожидаемых
					А В Ga , Gb - стандартное отклонение А и В. Для определения риска портфеля, состоящего из двух активов, используют стандартное отклонение портфеля (Gp), которое рассчитывают по следующей формуле:
					Wa - доля средств портфеля, инвестированная в актив А, Wb - доля средств портфеля, инвестированная в актив В. Коэффициента вариаций портфеля (Vqvab) рассчитывается как отношение стандартного отклонения
	портфеля к ожидаемой доходности портфеля:
				У Из нескольких альтернативных портфелей активов, предпочтение отдается тому портфелю, который имеет наименьший коэффициент вариации, т.е. имеет наименьший уровень риска на единицу доходности. Задача 2.2. На основе данных задачи 2.1 рассчитать показатели риска портфеля № 1, состоящего из 50 % акций А и 50 % акций В, и портфеля № 2, состоящего из 30 % актива А и 70 % актива В. Какой портфель является наиболее предпочтительнее с точки зрения оптимизации риска и доходности? Решение: I) На первом этапе рассчитываем ожидаемую доходность портфелей активов № 1 и 2, используя формулу 2.4: Г1 = 0,5*15+0,5*15=15 Г2 =0,3*15+0,7*15=15 26 Там же, С. 411. 27 Бригхэм Ю., Эрхард M Финансовый менеджмент. 10-е изд. / Пер. с англ. Под ред. К.э.н. Е.А. Дорофеева - СПб.: Питер, 2005. - С. 329.

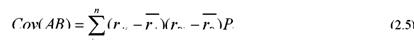
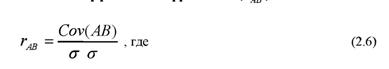
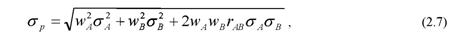
Первый портфель обладает более высоким риском по сравнению со вторым. Это происходит в результате того, что в первом портфеле удельный вес высокорискового актива «А» составляет 50%, в портфеле №2 - 30%

Вывод: Наиболее предпочтительным является второй портфель, т.к. он имеет коэффициент вариации.

Выбор оптимального портфеля ценных бумаг

Одной из важных задач, связанных с анализом портфелей ценных бумаг - это выбор оптимальных портфелей, определяемых как портфели, обеспечивающие наиболее высокую среднюю доходность при любой заданной степени риска или наименьший риск при любой заданной доходности.

На рисунке 2.1 представлено множество допустимых портфелей ценных бумаг. На рис. 2.1 граница области, заключенная между точками BCDE. определяет эффективное множество портфелей ценных бумаг, которое также и называется эффективной границей (efficient frontier). Портфели, расположенные слева от эффективного множества, недостижимы. Портфели же. расположенные справа от границы (внутренние), неэффективны, поскольку в этом случае найдутся другие портфели с тем же риском, но более высокой доходностью либо той же доходностью, но меньшим риском. Например, портфели ChD являются более предпочтительными по критерию «риск-доходность», чем X.

Рисунок 2.2 - Выбор оптимального портфеля рискованных активов.

Оптимальный для каждого инвестора портфель ценных бумаг на графике оказывается представлен точкой касания эффективного множества портфелей и одной из кривых безразличия инвестора. Эта кривая соответствует самому высокому уровню удовлетворенности, который может получить инвестор, используя достижимые для него портфели. Миссис У, которая более нерасположена к риску, чем мистер Z. выбирает портфель ценных бумаг с

ку ку 28

меньшей средней доходностью.

Одним из важнейших понятий в теории портфельных инвестиций является понятие «эффективный портфель», под которым понимается портфель, обеспечивающий максимальную ожидаемую доходность при некотором заданном уровне риска или минимальный риск при заданном уровне доходности. Алгоритм определения множества эффективных портфелей был разработан Г.Марковицем в 50-е годы как составная часть теории портфеля.. Сделанные им разработки были настолько фундаментальными, что по свидетельству известных специалистов в области портфельных инвестиций Э.Элтона и М.Грубера.

Очевидно, что эффективных портфелей может быть построено много, поэтому вводится понятие «оптимальный портфель». Основная идея определения оптимального портфеля в рамках теории Марковица может быть описана следующим образом. Инвестор строит для себя набор кривых безразличия, т.е. кривых, отражающих различные комбинации доходности и риска. Считается, что чем выше расположёна кривая, тем выше и уровень удовлетворенности, достигаемый инвестором.

Все комбинации, находящиеся на некоторой кривой безразличия, равно приемлемы для инвестора, т.е. он безразличен к выбору конкретной комбинации из набора. Далее строится набор эффективных портфелей (имеется в виду, что если инвестор имеет на выбор два портфеля одинакового риска, но с разной доходностью, то портфель, имеющий большую доходность, η будет эффективным). Оптимальным для инвестора будет портфель, характеризующийся точкой пересечения множества эффективных портфелей и одной из кривых безразличия.29

Вопросы для самоконтроля:

1. Дайте определение понятию «Риск». Перечислите основные характеристики риска.

2. Как измеряется риск актива и портфеля активов?

3. Что измеряет коэффициент корреляции и ковариации?

4. Какие портфели ценных бумаг из достижимого множества являются эффективными? Что такое эффективная граница портфелей?

5. Что такое кривые безразличия? Каким образом инвестор определяет для себя оптимальный портфель?

6. Какой портфель ценных бумаг является оптимальный?

Задачи для самостоятельной работы:

Задача 1. Предположим, что Ваши оценки возможной годовой доходности инвестирования в обыкновенные