ТЕОРЕТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ
При оценке пространственного распределения организмов на основе выборки из генеральной совокупности особое внимание следует обращать на соотношение размеров проб и агрегаций организмов на площади обследования.
Многими авторами (Greig- Smith, 1964; Cassie, 1963, и др ) было отмечено, что при обследовании одной и той же территории с помощью серий проб разного размера каждая серия может быть описана различными теоретическими распределениями. Так, использование очень маленьких или очень больших проб может привести к тому, что эмпирическое распределение будет соответствовать случайному, в то время как использование проб среднего размера покажет явную агрегированность распределения. Теоретические распределения хорошо описывают серии, полученные пробами, меньшими или большими, чем размер скоплений.Существует целый ряд теоретических распределений, которые могут быть использованы для описания эмпирических серий. Биномиальное распределение используют в том случае, если реальное размещение объектов может соответствовать регулярному, что, однако, редко встречается в природе Распределение Пуассона хорошо описывает случайное распределение организмов. Для описания агрегированных размещений исполь- 218
зуют отрицательное биномиальное распределение (Fisher, 1941) и распределения Неймана (Neyman, 1939) и Томас (Thomas, 1949). Установленное соответствие эмпирического распределения теоретическому позволяет использовать выборочные данные для дальнейшего статистического анализа после применения нормализующих преобразований, разработанных для каждого теоретического распределения (Barnes, 1952).
В том случае, если теоретические распределения включают параметры, имеющие биологический смысл (такие, как среднее количество агрегаций в пробе и среднее количество особей в агрегации), это позволяет получить наглядную картину реального распределения.
Однако оченьІчасто исследователи сталкиваются с тем случаем, когда при малой величине выборки эмпирическое распределение может статистически хорошо соответствовать чуть ли не всем теоретическим. Выбор же теоретического распределения часто ведётся наугад. Учитывая, что теоретические распределения строятся на разных предпосылках и большое значение имеет соотношение размера пробы и агрегаций, такое «соответствие» может привести к грубым ошибкам и неверным выводам,^Так, распределения Неймана и Томас предполагают случайное распределение компактных агрегаций на некоторой площади со случайным количеством особей в них. Как было показано Пиелоу (Pielou, 1957), корректное использование параметров этих распределений возможно только тогда, когда проба значительно превышает размер агрегаций. Для отрицательного биномиального распределения, которое может иметь место при изменении численности внутри агрегаций по логарифмическому закону, обязательным является другое соотношение размера пробы и агрегаций. Размер пробы обязательно должен быть меньше размеров агрегаций.Ранее (Смуров, 1975) было описано статистическое распределение с двумя параметрами: т — средней плотностью организмов на всей обследуемой территории; т— средней плотностью организмов в скоплениях.
Это распределение хорошо описывает тот случай, когда все организмы сосредоточены в скоплениях и распределение организмов внутри скоплений случайное[6]. Однако часто, особенно при исследовании популяций свободноподвижных организмов, приходится сталкиваться с тем, что в скоплениях находится только часть организмов, остальные же распределены вне скоплений, образуя фон с пониженной плотностью. Для точного описания таких распределений необходим дополнительный параметр, связанный с плотностью организмов вне скоплений. В печати сейчас находится статья, в которой даётся подробное математи-
ческоб оййсаййб такого ФрехпараМеТрйчёСкоГд распределений (Смуров, Романовский, в печати). В данной работе мы рассмотрим лишь основные свойства нового трёхпараметрического распределения.
Оно основано на следующих предпосылках. Предполагается, что на некоторой площади обследования S имеются произвольно расположенные скопления площади s{, со случайным распределением особей внутри скоплений; вне скоплений распределение особей также предполагается случайным. Средняя плотность особей внутри скоплений равна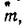
вне скоплений (на фоне) —
Тогда, если размер пробы меньше размера любого из скоплений, вероятность захвата случайной пробой (k) организмов будет равна:
где т — средняя плотность организмов на всей обследуемой территории, a k=0; 1; 2; 3... ^Средняя плотность по всей площади обследования может быть выражена как
чайной пробы на какое-либо из скоплений. Для реального пространственного распределения эта величина будет постоянной и в определённом интервале не зависящей от размера пробы. Это важнейшее свойство распределения, которое в дальнейшем будет использовано. Статистические моменты распределения следующие:
Величины центральных моментов второго
и третьего
порядков и среднюю _
J вычисляют по обычным применяемым в статистике формулам \ Параметры
находятся
1 См., например, Плохинский (1970) или Урбцх (1964).
220
Рис. 1. Зависимость коэффициента дисперсии от средней для ряда реальных распределений, описываемых различными теоретическими распределениями
А — Неймана ц Томас, Б — отрицательным биномиальным и трехпараметрическим, В — гипотетическим оеальныи при непрерывном изменении размера лроб выборок
Для отрицательного биномиального распределения:
где k — константа распределения.
Для нового трёхпараметрического распределения, учитывая, что
Видно, что у распределения Пуассона, Неймана, Томас зависимость дисперсии от средней — линейная, у нового распределения и отрицательного биномиального — квадратичная. Очевидно, что в том случае, когда реальное размещение организмов описывается распределениями Неймана или Томас, отношение дисперсии к средней не будет зависеть от величины средней и будет величиной постоянной (рис. 1, Л). Параметр отрицательного биномиального распределения, а также величина К и коэффициент b трехпараметрического распределения постоянны для реального размещения организмов и независятот величины средней; зависимость коэффициента дисперсии {о21т) от средней (щ) для этих распределений будет линейной (рис. 1, Б).
222
Если из популяции берётся несколько выборок, отличающихся размерами проб, то легко представить, что размер проб части выборок окажется меньше среднего раамера скоплений, а в других выборках размер проб превысит средний размер скоплений. В этом случае зависимость дисперсии от средней сначала может быть квадратичной, а затем перейдёт в линейную (рис.
1, В). В таком случае для выборок с малой величиной средних корректно использовать только трёхпараметрическое распределение и отрицательное биномиальное, а для выборок с большой величиной средних — распределения Неймана и Томас. Выборки со средними, близкими к точке перегиба, покажут плохое соответствие теоретическим распределениям Использование в исследованиях проб такого размера приведёт к неверным выводам.Обнаружив тот или иной характер зависимости дисперсии от средней, можно безошибочно применять нужное теоретическое распределение к выборочным данным Кроме этого, можно сразу установить соотношение размера пробы и размеров агрегаций. Технически зависимость дисперсии от средней легко установить, применив метод «последовательных квадратову Задачей этого метода, впервые описанного Грейг-Смитом (Greig- Smith, 1952), является установление размеров скоплений по характеру изменения дисперсий выборок в зависимости от размера проб. Однако даже в том случае, когда установить размер скоплений невозможно (скопления слишком велики), использование этого метода для установления зависимости дисперсии от средней поможет избежать ошибок, так как даст представление о реальной картине распределения организмов.