2. 1.1. Высказывания. Логические связки
Определение. Под высказыванием принято понимать языковое предложение, о котором имеет смысл говорить, что оно истинно или ложно в данный момент времени.
Высказывания чаще всего обозначают маленькими латинскими буквами a, b, c, х1, х2, …
В логике высказываний интересуются не содержанием, а истинностью или ложностью высказываний.
Истинностные значения – истина и ложь – будем обозначать И и Л соответственно. Множество {И, Л} называется множеством истинностных значений.Определение. Высказывание называют простым (элементарным), если оно рассматривается как некое неделимое целое (аналогично элементу множества). Сложным (составным) называется высказывание, составленное из простых с помощью логических связок.
В естественном языке роль связок при составлении сложных предложений из простых играют следующие грамматические средства: союзы «и», «или», «не»; слова «если …, то», «либо … либо», «тогда и только тогда, когда» и др. В логике высказываний логические связки, используемые для составления сложных высказываний, обязаны быть определены точно. Рассмотрим логические связки (операции) над высказываниями, при которых истинностные значения составных высказываний определяются только истинностными значениями составляющих высказываний, а не их смыслом.
|
| № набора | a |  |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
Определение.
Отрицанием высказывания является новое высказывание, истинное только тогда, когда исходное высказывание ложно (табл. 3).Отрицание обозначается через 
и читается как «не а», «неверно, что а».
Пример 15.
А – «Степан любит танцевать».
|
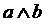- «Не верно, что Степан любит танцевать». | № набора | a | b | aÙb |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 1 | 1 |
Определение. Конъюнкцией двух высказываний является новое высказывание, которое истинно только тогда, когда оба исходных высказывания истинны (табл. 4).
Конъюнкция обозначается 
или a&b и читается как «a и b», «a, но b», «a, а b».
Пример 16.
а – «Степан любит танцевать», b – «Степан любит петь».
Тогда 
- «Степан любит танцевать и петь».
| № набора | a | b | aUb |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 1 |
| 3 | 1 | 1 | 1 |
 |
Определение. Дизъюнкцией двух высказываний является новое высказывание, которое ложно только тогда, когда оба исходных высказывания ложны (табл. 5).
Дизъюнкция обозначается через 
и читается как «a или b».
Пример 17.
а – «Степан любит танцевать», b – «Степан любит петь».
Тогда 
- «Степан любит танцевать или петь».
| № набора | a | b | a®b |
| 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 1 | 1 |
|
Импликация обозначается a® b и читается как «если a, то b»; « из а следует b». При этом a называется посылкой или условием, b – следствием или заключением.
Пример 18.
а – «Степан любит танцевать», b – «Степан любит петь».
Тогда 
- «Если Степан любит танцевать, то он любит петь».
| № набора | a | b | a»b |
| 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 1 | 1 |
|
Эквивалентность обозначается a» b и читается как «a эквивалентно b».
Пример 19.
а – «Степан любит танцевать», b – «Степан любит петь».
Тогда 
- «Для того, чтобы Степан любил танцевать, необходимо и достаточно, чтобы он любил петь».
Сведем все сказанное выше в единую таблицу и введем в рассмотрение еще три операции: сумма по модулю два, штрих Шеффера, стрелка Пирса (табл. 8).
Таблица 8
| Обозначения логической операции | Другие обозначения логической операции | Набор истинностных значений, отвечающих данной логической операции | Названия логической операции и связки | Как читается выражение, приведенное в первом столбце |
| O a | 10 | отрицание | неверно, что а; не а | |
| a Ù b | a & b a?b ab min(a; b) | 0001 | конъюнкция, логическое умножение, логическое «и» | a и b |
| aU b | a+b max(a; b) | 0111 | дизъюнкция, логическое сложение, логическое «или» | а или b |
| a® b | aEb a?b | 1101 | импликация, логическое следование | если а, то b; а имплицирует b; а влечет b |
| a » b | a º b a « b a Û b | 1001 | эквиваленция, эквивалентность, равнозначность, тождественность | а тогда и только тогда, когда b; а эквивалентно b |
| aA b | a+ b a D b | 0110 | сумма по модулю два, разделительная дизъюнкция, разделительное «или» | а плюс b; либо а, либо b |
| a ï b | 1110 | штрих Шеффера, антиконъюнкция | неверно, что а и b; а штрих Шеффера b | |
| a ¯ b | a o b | 1000 | стрелка Пирса, антидизъюнкция, функция Вебба, функция Даггера | ни а, ни b; а стрелка Пирса b |