§1.1. Высказывания
Высказыванием называется некоторое повествовательное утверждение, про которое можно однозначно сказать, истинно оно или ложно. Например, 
{число 50 делится на 10} – истина; 
{50 больше 100} – ложь.
Всякое высказывание является либо истинным, либо ложным (закон исключения третьего).
Никакое высказывание не может быть одновременно истинным и ложным (закон противоречия).
Отрицанием высказывания 
(обозначается ù или 
) называется высказывание, утверждающее, что высказывание не выполняется. Отрицание высказывания можно получить, сказав: “утверждение не имеет места” или “ не выполняется”. Определяющим словом здесь является частица “НЕ”.
Каково бы ни было высказывание , из двух высказываний и ù одно является истинным, а другое ложным.
Высказывание ù (ù) (или 
) называется двойным отрицанием высказывания . Имеет место равенство ù (ù) = (закон двойного отрицания).
Повествовательное утверждение, зависящее от некоторой переменной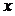 
и становящееся при конкретных значениях 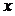высказыванием, называется неопределенным высказыванием (или предикатом). Неопределенное высказывание выражает некоторое свойство переменной .
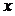Примеры предикатов. Пусть 
, 
, 
делится на 4}, 
{любой 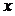-угольник можно разрезать на треугольники}. Здесь 
истинно, 
ложно, 
ложно, 
истинно, 
истинно, 
не имеет смысла.
Для неопределенного высказывания можно построить таблицу истинности. В таблице для конкретных значений переменной 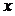указывается, истинно высказывание или ложно при этом 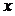. Например, 
{число 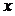делится на 3} истинно при любом 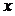, кратном 3, в
противном случае ложно.
Таблица истинности для предиката 
 |  |  |  |  |  |  |  |
| Ложь | Л | Истина | Л | Л | И | Л | |
Аналогично предикатам от одной переменной определяются предикаты от нескольких переменных: 
, 
и т.д.
Для предиката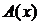 
можно построить высказывания “
” и “
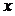” (читается: “для любого имеет место 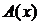” и “существует такое 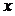, что имеет место ”).
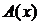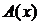верно при всех 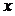, второе – когда 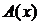верно хотя бы при одном 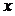. Символы “"” и “$” называются квантором всеобщности и квантором существования соответственно. Квантор всеобщности заменяется в словесных формулировках словами всякий, каждый, любой, все. Квантор существования заменяется в словесных формулировках словами существует, найдется, какой-нибудь, хотя бы один. С помощью кванторов можно образовывать также новые предикаты: если 
– предикат, то, например,
– предикат от 
,
– высказывание.
Выражения, содержащие кванторы, можно преобразовывать. Например, перестановка двух рядом стоящих одинаковых кванторов приводит к равносильному высказыванию:
;
º
.
Изменение же порядка следования кванторов существования и всеобщности друг с другом искажает смысл высказывания и может привести к изменению значения истинности. Так, например, на множестве натуральных чисел высказывания
(1) 
– истинно,
(2) 
– ложно.
Во многих вопросах математики возникает необходимость строить отрицание высказывания, выраженного с помощью кванторов.
Отрицания высказываний “” и “”.
Имеет место равенство ù 
º
ù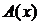. Действительно, утверждение “неверно, что для всех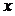 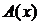” – это то же самое, что “для какого-нибудь 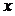не 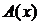”. Аналогично справедливо равенство ù 
º
ù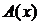, так как утверждение “неверно, что существует 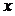, для которого 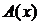” равносильно следующему: “для всех 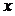не 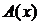”. Таким образом, чтобы построить отрицание высказывания, содержащего кванторы, надо кванторы 
заменить на 
, а на , а утверждение, стоящее под знаком кванторов, заменить на противоположное.
Пример. 
º
º
º
º
.