Важнейшие замкнутые классы
Введем следующие классы функций (классы Поста):
 ;
;  ;
;
 класс самодвойственных функций;
класс самодвойственных функций;
 класс монотонных функций (функция
класс монотонных функций (функция  называется монотонной);
называется монотонной);
 класс линейных функций (
класс линейных функций ( называется линейной).
называется линейной).
Лемма. Классы  замкнуты.
замкнуты.
Доказательство. а) Рассмотрим функцию  , где
, где  . Покажем, что
. Покажем, что  . Действительно,
. Действительно,
 .
.
Следовательно, класс  замкнут.
замкнут.
б) Аналогично предыдущему доказывается замкнутость класса  .
.
в) Пусть  , где
, где  самодвойственные функции. Тогда
самодвойственные функции. Тогда  , т. е. .
, т. е. .  . Следовательно, класс
. Следовательно, класс  замкнут.
замкнут.
г) Пусть  , где
, где  .
.
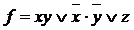 . Пусть
. Пусть 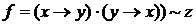
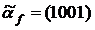
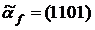 Наборы переменных состоят из переменных, встречающихся у функций
Наборы переменных состоят из переменных, встречающихся у функций 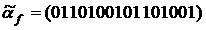
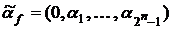 соответственно.
соответственно. Возьмем два набора  и
и  значений переменных
значений переменных  . Они определяют наборы
. Они определяют наборы  значений переменных
значений переменных  причем
причем  . Так как
. Так как  , то
, то
 .
.
Тогда  . Функция
. Функция  , поэтому
, поэтому  . Отсюда
. Отсюда
 .
.
Следовательно, класс  замкнут.
замкнут.
д) Класс  замкнут, так как линейное выражение, составленное из линейных выражений, является линейным.
замкнут, так как линейное выражение, составленное из линейных выражений, является линейным.
Лемма (о несамодвойственной функции). Если  , то из нее путем подстановки функций
, то из нее путем подстановки функций  и
и  вместо
вместо  можно получить несамодвойственную функцию одного переменного, т.е.
можно получить несамодвойственную функцию одного переменного, т.е.
Доказательство. Так как  , то существует набор
, то существует набор  такой, что
такой, что  .
.
Рассмотрим функцию  . Пусть
. Пусть
 .
.
Тогда

Следовательно,  константа 0 или 1.
константа 0 или 1.
Замечание. Если  , то вместо
, то вместо  подставляем
подставляем  , если же
, если же  то
то  .
.
Замечание. Для того чтобы определить, является ли функция 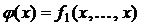 , заданная своим вектором значений
, заданная своим вектором значений  , самодвойственной, следует проверить, получается ли вторая половина вектора
, самодвойственной, следует проверить, получается ли вторая половина вектора  из первой отражением и последующим инвертированием его координат.
из первой отражением и последующим инвертированием его координат.
Лемма (о немонотонной функции). Если  , то подстановкой констант
, то подстановкой констант  ,
,  и функции
и функции  из нее можно получить
из нее можно получить  .
.
Доказательство. Если  , то найдутся два набора значений переменных
, то найдутся два набора значений переменных 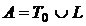 и
и 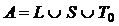 такие, что
такие, что  и
и  .
.
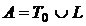 и
и 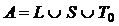 различаются в
различаются в 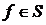 координатах (
координатах (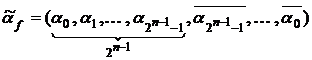 ), то, меняя по одной координате, между ними можно вставить
), то, меняя по одной координате, между ними можно вставить 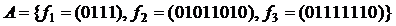 соседних наборов, т.е. таких, что
соседних наборов, т.е. таких, что 
и каждый следующий набор получается из предыдущего изменением ровно одной координаты.
Так как  , то в этой цепочке найдутся два соседних набора переменных
, то в этой цепочке найдутся два соседних набора переменных  и
и  такие, что
такие, что  и
и  . Пусть эти наборы различаются в
. Пусть эти наборы различаются в  - ой координате:
- ой координате:

 .
.
Рассмотрим функцию
 .
.
Имеем

Поскольку,  , то
, то  .
.
Замечание. Для проверки на монотонность функции 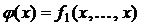 , заданной своим вектором значений
, заданной своим вектором значений  , нужно сначала разделить его две равные части
, нужно сначала разделить его две равные части  и
и  .
.
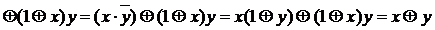 не выполнено, то
не выполнено, то 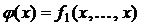 немонотонная. В противном случае разделим каждый из полученных векторов опять пополам
немонотонная. В противном случае разделим каждый из полученных векторов опять пополам 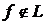 и
и 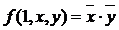 . Проверим сначала первую пару на выполнение соотношения
. Проверим сначала первую пару на выполнение соотношения 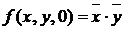 , и в случае положительного результата вторую. Если хотя бы для одной пары соотношение не выполняется, то функция немонотонная. В противном случае этот алгоритм продолжаем дальше.
, и в случае положительного результата вторую. Если хотя бы для одной пары соотношение не выполняется, то функция немонотонная. В противном случае этот алгоритм продолжаем дальше. Лемма (о нелинейной функции). Если  , то из нее путем подстановки констант
, то из нее путем подстановки констант  ,
,  и функций
и функций  и
и  , а также, быть может, инвертированием
, а также, быть может, инвертированием  , можно получить функцию
, можно получить функцию  .
.
Доказательство. Возьмем полином Жегалкина для  :
:
 .
.
В силу нелинейности полинома в нем найдется член, содержащий не менее двух множителей. Без ограничения общности можно считать, что среди этих множителей присутствуют  и
и  . Тогда можно преобразовать полином следующим образом:
. Тогда можно преобразовать полином следующим образом:

 ,
,
где в силу единственности полинома  .
.
Пусть  таковы, что
таковы, что  . Тогда
. Тогда
 ,
,
где  – константы, равные
– константы, равные  или
или  . Рассмотрим функцию
. Рассмотрим функцию  , получаемую из
, получаемую из  следующим образом:
следующим образом:
 .
.
Очевидно, что

 .
.
Следовательно,  .
.
Лемма. Классы Поста  попарно различны.
попарно различны.
Доказательство. Для доказательства леммы приведем функции, лежащие в классах, но так, чтобы классы взаимно не поглощались. Рассмотрим функции  и построим таблицу принадлежности классам. В таблице будем ставить «+», если функция принадлежит классу, и «–» в противном случае.
и построим таблицу принадлежности классам. В таблице будем ставить «+», если функция принадлежит классу, и «–» в противном случае.
 |  |  |  |  | |
| 0 | + | – | – | + | + |
| 1 | – | + | – | + | + |
 | – | – | + | – | + |
Если бы какие-нибудь два класса совпадали, то совпадали бы и соответствующие столбцы таблицы. Так как они не совпадают, делаем вывод о попарном различии классов.
Теорема Поста (о полноте). Для того чтобы система функций  была полной необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти замкнутых классов
была полной необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти замкнутых классов  .
.
Доказательство. Необходимость. Пусть система  полна. Тогда
полна. Тогда  . Допустим, что
. Допустим, что  содержится целиком в каком-либо из классов Поста (обозначим его через
содержится целиком в каком-либо из классов Поста (обозначим его через  ), т.е.
), т.е.  . В этом случае
. В этом случае  . Отсюда
. Отсюда  , что невозможно.
, что невозможно.
Достаточность. Пусть  не содержится целиком ни в одном из пяти классов Поста. Выделим из нее подсистему функций.
не содержится целиком ни в одном из пяти классов Поста. Выделим из нее подсистему функций.  , где
, где 
 , и на ее основе построим полную систему.
, и на ее основе построим полную систему.
1. При помощи  построим функции (константы) 0 и 1 или функцию
построим функции (константы) 0 и 1 или функцию  .
.
Разберем отдельно два случая:
(а)  ;
;
(б)  .
.
(а) Рассмотрим функцию  . Из цепочки равенств
. Из цепочки равенств  следует, что
следует, что  .
.
(б) В этом случае для функции  получаем
получаем  , т.е.
, т.е.  .
.
Аналогичным образом, используя функцию  , строим константу 0 или функцию
, строим константу 0 или функцию  .
.
Итак, нами построены либо функция  , либо обе константы 0 и 1. или
, либо обе константы 0 и 1. или
2. Если построена  , то с помощью
, то с помощью  и
и  , применяя лемму о несамодвойственной функции, строим константы 0 и 1.
, применяя лемму о несамодвойственной функции, строим константы 0 и 1.
Если есть обе константы 0 и 1, то .с помощью функций 0, 1 и  , используя лемму о немонотонной функции, можно построить
, используя лемму о немонотонной функции, можно построить  .
.
3. При помощи 0, 1,  и
и  , применяя лемму о нелинейной функции, строим функцию
, применяя лемму о нелинейной функции, строим функцию  .
.
Система  полная. Значит, и
полная. Значит, и  полная. Отсюда следует полнота системы
полная. Отсюда следует полнота системы  . Теорема доказана.
. Теорема доказана.
Следствие 1. Из всякой полной системы можно выделить полную подсистему, содержащую не более пяти функций.
Это утверждение можно усилить, а именно, имеет место.
Лемма. Из всякой полной системы можно выделить полную подсистему, содержащую не более четырех функций.
Доказательство. Так как  , то либо
, то либо  либо
либо  . Тогда полная система будет состоять из функций
. Тогда полная система будет состоять из функций  либо
либо  .
.
Пример 1. Определить количество функций классов  и
и  , зависящих от переменных
, зависящих от переменных  .
.
Решение. Вектор значений функции  имеет вид
имеет вид  , т.е. определено только значение на нулевом
, т.е. определено только значение на нулевом
наборе переменных, свободных же  . Следовательно,
. Следовательно,  . Аналогично вычисляется количество функций класса
. Аналогично вычисляется количество функций класса  .
.
Пример 2. Определить количество самодвойственных функций, зависящих от  переменных.
переменных.
Решение. Функция  принимают противоположные значения на противоположных наборах переменных. Поэтому для ее задания достаточно задать первую половину ее вектора значений
принимают противоположные значения на противоположных наборах переменных. Поэтому для ее задания достаточно задать первую половину ее вектора значений  . Следовательно, количество самодвойственных функций, зависящих от
. Следовательно, количество самодвойственных функций, зависящих от  переменных, равно
переменных, равно  .
.
Пример 3. Определить количество линейных функций, зависящих от переменных  .
.
Решение. Различных линейных функций от переменных  столько же, сколько различных векторов
столько же, сколько различных векторов  , т.е.
, т.е.  . Задачи для самостоятельного решения.
. Задачи для самостоятельного решения.
1. Перечислить все самодвойственные функции от двух переменных.
2. Выяснить, является ли самодвойственной функция  :
:
а)  ;
;
б)  ;
;
в)  .
.
3. Выяснить, является ли самодвойственной функция  , заданная векторно:
, заданная векторно:
а)  ; б)
; б)  ;
;
в)  ;
;
г)  .
.
4. Определить, какие из переменных функций 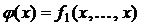 следует заменить на
следует заменить на  , а какие на
, а какие на  с тем, чтобы получить константу:
с тем, чтобы получить константу:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
5. Выяснить при каких  функция
функция  :
:
а)  ;
;
б)  ;
;
в)  .
.
6. Перечислить все линейные функции от двух переменных.
7. Представив функцию  полиномом, выяснить, является ли она линейной:
полиномом, выяснить, является ли она линейной:
а)  ;
;
б)  ;
;
в)  .
.
8. Выяснить, является ли линейной функция  , заданная векторно:
, заданная векторно:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
9. Подставляя на места переменных нелинейной функции 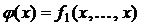 функции из множества
функции из множества  , получить хотя бы одну из функций
, получить хотя бы одну из функций  :
:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
10. Найти число линейных функций 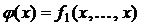 ,
,
а) существенно зависящих в точности от  переменных;
переменных;
б) удовлетворяющих условию  .
.
11. Выяснить, принадлежит множеству  функция
функция 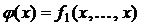 :
:
а)  ;
;
б)  .
.
12. Выяснить, при каких  функция
функция  :
:
а)  ;
;
б)  .
.
13. Приведите все монотонные функции от двух переменных.
14. Выяснить, является ли монотонной функция  :
:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
15. Выяснить, является ли монотонной функция  , заданная векторно:
, заданная векторно:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
16. Для немонотонной функции 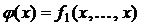 указать два соседних набора
указать два соседних набора  и
и  значений переменных таких, что
значений переменных таких, что и
и  :
:
а)  ;
;
б)  ;
;
в)  .
.
17. Выяснить при каких  функция
функция 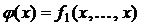 монотонна:
монотонна:
а)  ; б)
; б)  .
.
18. Подсчитать число функций, зависящих от переменных  и принадлежащих множеству
и принадлежащих множеству  :
:
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  .
.
19. Выяснить, полна ли система функций  :
:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  . Ответы
. Ответы
1.  . 2. а)
. 2. а)  ; б)
; б)  ; в)
; в)  . 3. а)
. 3. а)  ;
;
б)  ; в)
; в)  ; г)
; г)  . 4. а)
. 4. а)  заменить на
заменить на  ,
,  на
на  или наоборот; б) существуют две пары наборов таких, что
или наоборот; б) существуют две пары наборов таких, что  : (010) – (101) и (011) – (100). В первом случае заменив
: (010) – (101) и (011) – (100). В первом случае заменив  на
на  , а
, а  на
на  получим константу 0; во втором заменив
получим константу 0; во втором заменив  на
на  , а
, а  на
на  получим константу 1; в) получим константу 1, заменив, например,
получим константу 1; в) получим константу 1, заменив, например,  на
на  , а
, а  на
на  получим константу 0; во втором заменив
получим константу 0; во втором заменив  на
на  , а
, а  на
на  ; г) существуют три пары наборов таких, что
; г) существуют три пары наборов таких, что  : (0011) – (1100), (0100) – (1011) и (0110) – (1110). Можем координаты, соответствующие 0 в первом наборе каждой пары заменить на
: (0011) – (1100), (0100) – (1011) и (0110) – (1110). Можем координаты, соответствующие 0 в первом наборе каждой пары заменить на  , а соответствующие 1 – на
, а соответствующие 1 – на  . 5. а) при нечетных
. 5. а) при нечетных  ; б) – в) при всех
; б) – в) при всех 
 . 6.
. 6.  . 7. а)
. 7. а) 

 ; б)
; б)  ; в)
; в)  . 8.а)
. 8.а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  . 9. а)
. 9. а)  ; б)
; б)  ; в)
; в)  ;
;
г)  . 10. а)
. 10. а)  б)
б)  . 11. а)
. 11. а)  ;
;
б)  . 12. а) при нечетных
. 12. а) при нечетных  ; б) при всех
; б) при всех  и
и 
 . 13.
. 13.  . 14. а)
. 14. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  . 15. а)
. 15. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  . 16. а)
. 16. а)  ,
,  ; б)
; б)  ,
,  или
или  ;
;  ,
,  или
или  ;
;
в)  ,
,  .
.
17. а) при 
 , при
, при 
 б) при
б) при  и
и  при всех
при всех  .
.  . 18. а)
. 18. а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  . 19. а) Нет.
. 19. а) Нет.  . б) Нет.
. б) Нет.  . в) Нет.
. в) Нет.  . г) Да. д) Да. е) Нет.
. г) Да. д) Да. е) Нет.  .
.