Теорема о цикломатическом числе
Напомним, что цикломатическим числом графа G называется число 
, где 
– число ребер, 
– число вершин, 
– число компонент связности графа G.
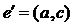, для дерева 
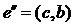. Теорема. Если граф 
состоит из нескольких компонент связности 
, то 
.
Доказательство. Так как графы – связные графы, то 
, …, 
. Сложив почленно эти равенства, получим 
. Теорема доказана.
Введем определение суммы циклов произвольного графа. Пусть С1 и С2 – произвольные циклы графа G, содержащие общие участки пути, соединяющие вершины 
и 
, 
и 
и так далее. Тогда суммой циклов С1 и С2 будем называть граф, вершинами которого являются все вершины циклов С1 и С2, за исключением внутренних вершин их общих участков, а ребрами – все их ребра, за исключением ребер, составляющих их общие участки (рис.
, 
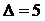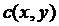. По сложению циклы образуют абелеву группу. Если граф G имеет т ребер е1, е1, … ет, то любому циклу С графа G можно поставить в соответствие двоичный код длины т: 
, 
Если циклу С1 соответствует код 
, а циклу С2 – код 
, то циклу С1+С2 соответствует код 
, где сложение производится по модулю 2. Таким образом, множество циклов графа G можно рассматривать, как подгруппу группы 
. Циклы образуют линейное пространство над полем 
.
Теорема. Пусть дан произвольный граф G (без петель, без кратных ребер, с конечным числом вершин) и 
. Тогда:
1) Из графа G можно удалить k ребер так, что оставшийся граф будет без циклов и будет иметь столько же компонент связности, что и G.
2) Размерность пространства циклов графа G равна k.
Доказательство. 
. Докажем, что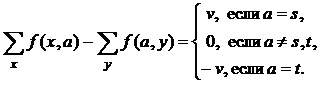 
тогда только тогда, когда в графе G нет циклов.
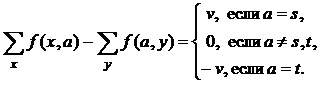, а 
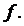– компоненты связности графа G, то 
. Так как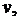 
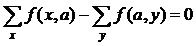, то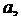 
при всяком 
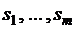. Имеем 
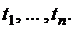, следовательно, 
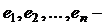– дерево, а значит, в 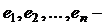нет циклов. Таким образом, в графе G тоже нет циклов. Докажем, что если в графе G нет циклов, то 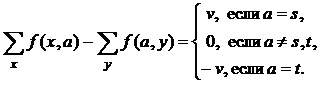. Действительно, тогда G – лес, 
, где ,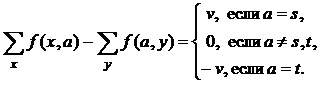 
– компоненты связности графа G, т.е. деревья. Так как для дерева 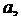, то .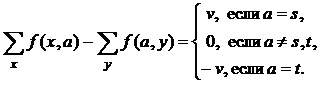
Таким образом, мы доказали, что если для графа G 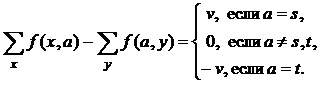, то в нем нет циклов.
Пусть теперь 
. Тогда в G есть циклы. Возьмем произвольно цикл С1, е1 – произвольное ребро этого цикла. Тогда граф 
имеет то же количество компонент связности, что и G. 
.
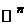, то полученный граф будет без циклов. Если 
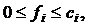, то аналогично берем цикл С2 и ребро е2 и т.д. Этот процесс состоит ровно из 
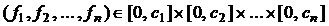шагов. На каждом шаге количество компонент связности не меняется. Граф 
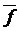является лесом, количество компонент связности у него такое же, как и у G. 
. Занумеруем остальные ребра графа G: 
. Тогда циклам С1, …,Сk соответствуют коды
Строки кодов линейно независимы. Осталось доказать, что любой цикл графа G можно линейно выразить через циклы С1, С2, …, Сk.. Возьмем произвольный цикл С с соответствующим ему кодом 
. Строки
линейно независимы, следовательно, образуют базис в пространстве размерности k. Поэтому
при некоторых 
. Рассмотрим цикл
.
Учитывая, что 
, получаем
Таким образом, 
– цикл в графе 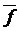. Но по построению, 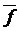– граф без циклов.
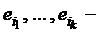и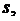 
, значит, 
.
Теорема доказана.
Если G – связный граф и , то по только что доказанной теореме из G можно удалить некоторые k ребер так, чтобы получилось дерево Т. Назовем его остовным деревом графа G. Аналогично, если G – несвязный граф, то из G можно удалить некоторые k ребер так, чтобы получился граф без циклов, т.е. лес, называемый остовным лесом графа G. 
Решение типовых задач
1. Существует ли Эйлеров цикл у графа, изображенного на рис. 2.41? Если существует, построить его.
Решение. Так как степени всех вершин четны, тот эйлеров цикл существует. Возьмем произвольный цикл, например, (1, 5, 3, 1). Этот цикл не содержит все ребра графа. Рассмотрим граф, полученный из исходного удалением этого цикла. Удаленный граф и оставшийся, в силу связности исходного графа всегда имеют общую вершину, в данном случае – 5. Рассмотрим теперь произвольный цикл нового графа, начинающийся в вершине 5, например, (5, 4, 6, 5). Присоединим его к первому циклу: (1, 5, 4, 6, 5, 3, 1). Остается единственный цикл (4, 1, 2, 4), присоединив который, получим эйлеров цикл (1, 5, 4, 1, 2, 4, 6, 5, 3, 1).
2. Найти число компонент связности леса, который имеет 40 вершин и 23 ребра.
Решение. Так как для леса 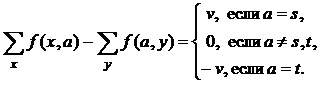, получаем 
, 
.
3. Чему может равняться число ребер графа, имеющего 20 вершин и 4 компоненты связности?
Решение. Так как , имеем 
, следовательно, 
. Покажем, что найдется граф, для которого 
, 
, 
.
Докажем, что наибольшее количество ребер у графа, три компоненты связности которого представляют собой изолированные вершины, четвертая – полны граф К17 с числом ребер, равным 136. Действительно, рассмотрим граф с 20 вершинами и 4 компонентами связности 
, из которых по крайней мере 2 содержат не менее двух вершин. Предположим, что 
. Возьмем произвольно вершину из 
, удалим все ребра, инцидентные ей, и соединим ее ребрами со всеми вершинами из 
. Новый граф будет иметь то же количество вершин и компонент связности, но больше ребер. Таким образом, количество ребер может быть от 16 до 136.
4. Чему может равняться число компонент связности графа, имеющего 12 вершин и 27 ребер?
Решение. Так как простая цепь С12 имеет 11 ребер, а полный граф К12 – 66 ребер, то существует связный граф, имеющий 12 вершин и 27 ребер. Минимальное число компонент связности равно 1. Для того, чтобы определить максимально возможное число компонент связности, найдем наименьший полный граф, число ребер которого не меньше 27: 
. Рассмотрим граф, 4 компоненты связности представляют собой изолированные вершины, а пятая имеет 8 вершин и 27 ребер. Докажем, что 6 компонент связности быть уже не может. Действительно, по предыдущей задаче, граф, имеющий 12 вершин и 6 компонент связности, может иметь не более 21 ребра. Таким образом Таким образом, количество компонент связности может быть от 1 до 5.
5. Для графа, изображенного на рис.2.42(а) найти цикломатическое число, укзать базис циклов, построить остовное дерево.
Для данного графа 
, 
, 
. Следовательно, 
и из 
надо удалить три ребра, чтобы получилось дерево. Базис циклов также состоит из трех циклов. Выберем произвольно цикл, например, 
. Удалим из графа ребро е2. В получившемся графе возьмем цикл 
. Удалим из графа ребро е5. В получившемся графе возьмем цикл 
. Удалим из графа ребро е10. Получим остовное дерево графа , изображенное на рис. 2.42б). Циклы С1, С2, С3 образуют базис. Разложим какой-нибудь цикл, например, 
, по этому базису. Запишем коды циклов:
Так как были удалены ребра е2, е5, е10, то в матрице, составленной из кодов циклов С1, С2, С3, С4, базисным будет минор, составленный из столбцов под номерами 2, 5, 10: 
.
Отсюда получаем 
. Задачи для самостоятельного решения
1. Сколько компонент связности имеет граф со следующим набором степеней вершин: 1, 1, 1, 2, 2, 2, 2, 3?
2. Изобразить граф 
. Найти 
, построить базис циклов.
3. Изобразить граф 
. Найти , построить базис циклов.
4. Построить базис циклов графа 
.
5. Построить базис циклов графа 
.
6. Построить базис циклов графа 
.
7. Построить базис циклов графа 
.
8. Является ли деревом прямое произведение деревьев?
9. Найти число компонент связности леса, который имеет 76 вершин и 53 ребра.
10. Сколько ребер имеет лес с 10 вершинами, если он имеет 3 компоненты связности?
11. Чему может равняться число компонент связности графа, имеющего 15 вершин и 35 ребер?
12. Чему может равняться число компонент связности графа, имеющего 12 вершин и 20 ребер?
13. Чему может равняться число ребер графа, имеющего 10 вершин и 3 компоненты связности?
14. Доказать, что если граф имеет 10 вершин и 37 ребер, то он связен.
15. Доказать, что если граф имеет 8 вершин и 23 ребра, то он связен.
16. Связный граф имеет 12 вершин. Сколько он может иметь ребер?
17. Сколько ребер может быть у связного графа с п вершинами?
18. Сколько всего неизоморфных деревьев с пятью вершинами? Изобразить их.
19. Сколько всего графов с 12 вершинами и 65 ребрами? с 64 ребрами?
20. Построить коды деревьев (два для каждого дерева), изображенных на рис. 2.43.
21. Построить дерево по коду (00101001011101).
22. Построить дерево по коду (00101011001101).
23. Построить дерево по коду [5345566].
24. Построить дерево по коду [4445477].
25.
 |
У каких из графов, изображенных на рис. 2.44, существует эйлеров путь или эйлеров цикл? Если существует, то построить его.
 |
Ответы
1. 1 или 2. Указание. Рассмотреть, сколько вершин может быть в каждой компоненте связности. 2. См. рис. 2.45. 
. Базис циклов: (1, 2, 3), (1, 3, 6, 4), (3, 2, 5, 6), (1, 2, 5, 4). 3. 
. 4. 
.
5. 
. 6. 
. 7. . 8. Не является (см. рис. 2.12).
9. 23. 10. 7. 11. От 1 до 7. 12. От 1 до 6. 13. От 7 до 28. 14. Указание. Доказать, что несвязный граф с 10 вершинами имеет не более 36 ребер. 15. Указание. Доказать, что несвязный граф с 8 вершинами имеет не более 21 ребра. 16. От 11 до 66. 17. От 
до 
. 18. 3 , см рис. 2.46. Указание. Рассмотреть возможные наборы степеней вершин. 19. Один, два. 20. При нумерации, указанной на рис. 2.47:
а) (01000010110101101101), [114457557]; б) (0000101110010111); [2332477]; в) (0010100101011011), [ 4444666];
г) (00001010101111), [246666]. 21. См. рис. 2.48а . 22. См. рис. 2.48б.
 |
23. См. рис. 2.48в. 24. См. рис. 2.48г. 25. а), в) – существует; б) нет.
|
