§2.3. Связность
Граф называется связным, если любые две несовпадающие вершины в нем соединены маршрутом.
Очевидно, для связности графа необходимо и достаточно, чтобы в нем для какой-либо фиксированной вершины и и каждой другой вершины v существовал (u, v)-путь.
Пусть задан граф G. Введем на множестве его вершин V(G) бинарное отношение. Будем говорить, что 
, если существует путь из 
в 
. При этом будет считать, что 
, их соединяет путь нулевой длины. Введенное отношение является отношением эквивалентности. Следовательно, оно определяет разбиение множества вершин графа на классы эквивалентности: 
. Обозначим через 
подграф графа 
, порожденный множеством вершин 
. При этом
, 
, 
.
Графы 
называются компонентами связности графа .
Теорема. Для любого графа либо он сам, либо его дополнение является связным.
Доказательство. Пусть G – несвязный граф. А – одна из его компонент связности. Положим В = VG \ VA. Возьмем произвольную вершину и графа А.
Тогда для любой вершины v из из множества вершин В в дополнительном графе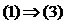
есть ребро uv. Следовательно, произвольная вершина из В соединена с и. Если и1 – отличная от и вершина графа А, то для любой вершины v из множества вершин В в дополнительном графе 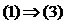также найдется ребро u1v. Таким образом найдется путь из вершины и в вершину u1 (через вершину v). Следовательно, из вершины и в графе 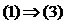достижима любая вершина, а значит, граф 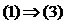является связным. Теорема доказана. Утверждение. Пусть G – связный граф, 
. Тогда:
1) если ребро е принадлежит какому-либо циклу графа G, то граф 
связен;
2) если ребро е не входит ни в какой цикл, то граф имеет ровно две компоненты связности.
Доказательство. 1). Пусть ребро 
принадлежит циклу Z графа G. Заменив в каждой 
-цепи, содержащей е, ребро е на цепь 
, получим путь, соединяющий вершины х и у, не содержащий ребра е. Следовательно, для любых двух несовпадающих вершин в графе G найдется -путь, не включающий ребро е. Но тогда и граф связен.
2) Пусть ребро е не входит ни в какой цикл графа G. Тогда, очевидно, вершины и и v входят в разные компоненты связности графа .
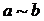и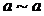 
соответственно. Для произвольной вершины 
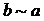в G найдется 
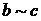-путь. Если ребро е в этот путь не входит, то 
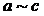. В противном случае 
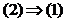. Утверждение доказано. Обозначим через Р количество ребер графа, В – количество вершин, K – количество компонент связности. Число 
называется цикломатическим числом графа.
Теорема. Для любого графа выполняется неравенство
Доказательство проведем индукцией по числу вершин п. При п = 1 получаем граф, состоящий из одной вершины, соответственно без ребер: 
. Неравенство
выполнено.
Предположим, что при любом количестве вершин, меньшем п, утверждение верно и докажем его для графа с п вершинами. Обозначим их 
. Обозначим через 
подграф графа , порожденный вершинами 
. Тогда 
по предположению индукции. Пусть 
– количество ребер, вершин, компонент связности графа ; 
– графа ; k – количество ребер графа , не являющихся ребрами графа 
, т.е.
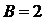. Тогда 
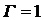. Возможны два случая. а) 
, следовательно, вершина 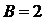– изолированная. При этом 
. Следовательно, 
, 
.
б) 
. Если при этом все k ребер, инцидентных вершине 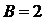, соединяют ее с различными компонентами связности графа , то 
, в остальных случаях 
. Таким образом,
. В итоге получаем 
. Теорема доказана.
Следствие. Для связного графа выполняется неравенство 
.