Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы
Ведем обозначение 
Выражение  , где
, где  какой-либо двоичный набор, причем среди переменных
какой-либо двоичный набор, причем среди переменных  могут быть совпадающие, называется элементарной конъюнкцией.
могут быть совпадающие, называется элементарной конъюнкцией.
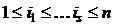 называют буквами. Число букв в элементарной конъюнкции называют рангом элементарной конъюнкции.
называют буквами. Число букв в элементарной конъюнкции называют рангом элементарной конъюнкции. Элементарная конъюнкция
– правильная, если в нее каждая переменная входит не более одного раза (включая и отрицание переменной);
– полная относительно переменных  , если в нее каждая переменная (или ее отрицание) входит ровно один раз;
, если в нее каждая переменная (или ее отрицание) входит ровно один раз;
– монотонная, если она не содержит отрицаний переменных.
Формула вида  , где
, где  попарно различные элементарные конъюнкции, называется дизъюнктивной нормальной формой (сокращенно ДНФ). Число
попарно различные элементарные конъюнкции, называется дизъюнктивной нормальной формой (сокращенно ДНФ). Число 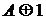 называется длиной ДНФ.
называется длиной ДНФ.
Теорема. Каждую булеву функцию  при любом
при любом 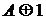 (
( ) можно представить в виде
) можно представить в виде
 (*)
(*)
Это представление называется разложением функции по переменным  .
.
Доказательство.
Заметим, что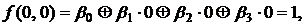 Далее рассмотрим произвольный набор
Далее рассмотрим произвольный набор 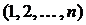 и покажем, что левая и правая часть формулы (
и покажем, что левая и правая часть формулы (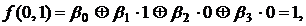 ) принимают на нем одно и то же значение.
) принимают на нем одно и то же значение. Левая часть дает  , а правая
, а правая

Следствие 1. Разложение по переменной  . Пусть
. Пусть  . Тогда
. Тогда

Следствие 2. Разложение по всем переменным. Пусть . Тогда
. Тогда

При  получаем выражение
получаем выражение

т.е.

Разложение (**) носит название совершенной дизъюнктивной нормальной формы (СДНФ).
Замечания 1. Поскольку существует взаимно однозначное соответствие между таблицей истинности  и СДНФ функции
и СДНФ функции  , то СДНФ функции единственна.
, то СДНФ функции единственна.
2. Единственная функция, не имеющая СДНФ, – константа 0.
3. Длина СДНФ функции  равна числу наборов, на которых функция принимает значение, равное 1.
равна числу наборов, на которых функция принимает значение, равное 1.
Пример. Построить СДНФ функций:
а)  ;
;
б)  .
.
Табл.
1.9 |  |  |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Решение. а) Из таблицы 1.9 получаем, что  на наборах
на наборах 
 . Поэтому
. Поэтому 

Табл. 1.10
 |  |  |  |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
б) Из таблицы истинности заданной функции  (табл. 1.10) видим, что значение функции равно 1 только на двух наборах. СДНФ функции имеет вид
(табл. 1.10) видим, что значение функции равно 1 только на двух наборах. СДНФ функции имеет вид 
Замечание.
По данной ДНФ функции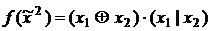 можно построить ее СДНФ. Для этого достаточно «пополнить» каждую конъюнкцию недостающими буквами
можно построить ее СДНФ. Для этого достаточно «пополнить» каждую конъюнкцию недостающими буквами 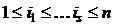 , применяя соотношение
, применяя соотношение 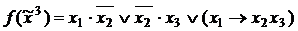 , а затем устранить повторения, применив эквивалентность
, а затем устранить повторения, применив эквивалентность 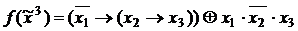 .
. Теорема. Каждая функция алгебры логики может быть выражена в виде отрицания, конъюнкции и дизъюнкции.
Доказательство. Пусть  , тогда
, тогда  .
.
Если  , то выразим ее в виде СДНФ
, то выразим ее в виде СДНФ

Следовательно, в обоих случаях функция  выражается в виде формулы через отрицание, конъюнкцию и дизъюнкцию.
выражается в виде формулы через отрицание, конъюнкцию и дизъюнкцию.
Выражение  , где
, где  какой-либо двоичный набор, причем среди переменных
какой-либо двоичный набор, причем среди переменных  могут быть совпадающие, называется элементарной дизъюнкцией.
могут быть совпадающие, называется элементарной дизъюнкцией.
Элементарная дизъюнкция
– правильная, если в нее каждая переменная входит не более одного раза (включая и отрицание переменной);
– полная относительно переменных  , если в нее каждая переменная (или ее отрицание) входит ровно один раз.
, если в нее каждая переменная (или ее отрицание) входит ровно один раз.
Формула вида  , где
, где  попарно различные элементарные дизъюнкции, называется конъюнктивной нормальной формой (сокращенно КНФ).
попарно различные элементарные дизъюнкции, называется конъюнктивной нормальной формой (сокращенно КНФ).
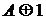 называется длиной КНФ.
называется длиной КНФ. В соответствии с принципом двойственности для функции можно получить следующее выражение для  :
:

Для доказательства этого рассмотрим функцию, двойственную к функции  . В соответствии с формулой (*) для нее получим:
. В соответствии с формулой (*) для нее получим:

Из тождества для двойственных формул получим
 Поскольку
Поскольку  и
и  , то получаем формулу (***).
, то получаем формулу (***).
Для  и
и  получаем выражение
получаем выражение

которое носит название совершенной конъюнктивной нормальной формы (СКНФ).
Замечания: 1. СКНФ функции единственна.
2. Единственная функция, не имеющая СКНФ, – константа 1.
3. Длина СКНФ функции  равна числу наборов, на которых функция принимает значение, равное 0.
равна числу наборов, на которых функция принимает значение, равное 0.
Пример. Построить СДНФ функции  .
.
Решение. Исходя из таблицы 1.9, получим, что  на одном наборе
на одном наборе  . Поэтому
. Поэтому 

Замечание. По данной КНФ функции  можно построить СКНФ функции. Для этого достаточно «пополнить» каждую из дизъюнкций недостающими буквами
можно построить СКНФ функции. Для этого достаточно «пополнить» каждую из дизъюнкций недостающими буквами 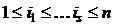 , применяя соотношение
, применяя соотношение  , а затем устранить повторения с помощью эквивалентности
, а затем устранить повторения с помощью эквивалентности  .
.