Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы
Рассмотрим произвольную 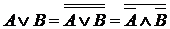 -членную операцию
-членную операцию  , заданную своей таблицы значений, не являющуюся противоречием.
, заданную своей таблицы значений, не являющуюся противоречием.
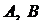 принимает значения “И”. Для каждой строки составим элементарные конъюнкции из
принимает значения “И”. Для каждой строки составим элементарные конъюнкции из 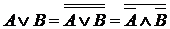 множителей, где
множителей, где 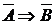 -й множитель равен
-й множитель равен 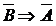 (в этой строке
(в этой строке 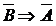 принимает значение “И”) или
принимает значение “И”) или 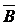 (в этой строке
(в этой строке 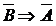 принимает значение “Л”). Далее возьмем дизъюнкцию всех полученных конъюнкций. В итоге получится формула (д. н. ф. ), задающая операцию, равносильную
принимает значение “Л”). Далее возьмем дизъюнкцию всех полученных конъюнкций. В итоге получится формула (д. н. ф. ), задающая операцию, равносильную 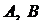 . Действительно, каждая из построенных конъюнкций будет истинна только при тех значениях истинности высказываний
. Действительно, каждая из построенных конъюнкций будет истинна только при тех значениях истинности высказываний 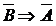 , которые стоят в соответствующей строчке. Поскольку была взята дизъюнкция по всем наборам значений истинности высказываний
, которые стоят в соответствующей строчке. Поскольку была взята дизъюнкция по всем наборам значений истинности высказываний 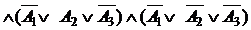 , на которых
, на которых 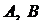 истинна, то построенное высказывание истинно на всех этих наборах и только на них. На остальных наборах оно ложно.
истинна, то построенное высказывание истинно на всех этих наборах и только на них. На остальных наборах оно ложно. Построенная формула называется совершенной дизъюнктивной нормальной формой (СДНФ) операции  .
.
Аналогично, рассматривая строки, в которых операция 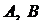 , не являющаяся тавтологией, принимает значения “Л”, и составляя конъюнкцию (число множителей равно числу отмеченных строк таблицы) дизъюнкций из
, не являющаяся тавтологией, принимает значения “Л”, и составляя конъюнкцию (число множителей равно числу отмеченных строк таблицы) дизъюнкций из 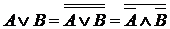 слагаемых, где
слагаемых, где 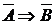 -е слагаемое равно
-е слагаемое равно 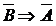 (в этой строке
(в этой строке 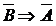 принимает значение “Л”) или
принимает значение “Л”) или 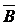 (в этой строке
(в этой строке 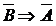 принимает значение “И”). В итоге получится формула, задающая операцию, равносильную
принимает значение “И”). В итоге получится формула, задающая операцию, равносильную 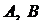 . Построенная формула называется совершенной конъюнктивной нормальной формой (СКНФ) операции
. Построенная формула называется совершенной конъюнктивной нормальной формой (СКНФ) операции  .
.
Пример. Построить СДНФ и СКНФ операции, заданной таблицей истинности.
 |  |  |  |
| И | И | И | Л |
| И | И | Л | И |
| И | Л | И | Л |
| И | Л | Л | И |
| Л | И | И | Л |
| Л | И | Л | Л |
| Л | Л | И | Л |
| Л | Л | Л | И |
Решение. Операция  принимает значение “И” только на трех наборах, а “Л” на пяти наборах.
принимает значение “И” только на трех наборах, а “Л” на пяти наборах.
СДНФ= ;
;
СКНФ=
 .
.
Теорема 3. Любая логическая операция может быть выражена через операции отрицания и конъюнкции.
Доказательство. Выразим дизъюнкцию через операции отрицания и конъюнкции, используя закон двойного отрицания и закон де Моргана:  .
.
Найдя СДНФ или СКНФ данной операции и заменив в них дизъюнкцию через операции отрицания и конъюнкции, получим формулу, содержащую только операции отрицания и конъюнкции. Теоремы
Теоремы в математике чаще всего формулируются в виде « », где
», где 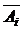 – условие теоремы (то, что дано), а
– условие теоремы (то, что дано), а 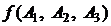 – заключение (то, что утверждается).
– заключение (то, что утверждается). 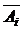 и
и 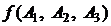 являются высказываниями (возможно, неопределенными).
являются высказываниями (возможно, неопределенными).
При доказательстве теоремы в предположении истинности посылки устанавливается истинность заключения.
Всякое высказывание, из которого следует истинность высказывания 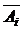 , называется достаточным условием для
, называется достаточным условием для 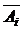 . Всякое высказывание, истинность которого следует из истинности высказывания
. Всякое высказывание, истинность которого следует из истинности высказывания 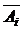 , называется необходимым условием для
, называется необходимым условием для 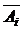 . Итак
. Итак 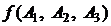 необходимо для
необходимо для 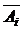 , если истинна импликация
, если истинна импликация  .
.
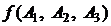 достаточно для
достаточно для 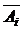 , если верна импликация
, если верна импликация 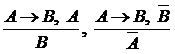 .
. Теоремы  и
и 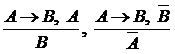 называются обратными друг другу. Первую называют прямой теоремой, другую – обратной.
называются обратными друг другу. Первую называют прямой теоремой, другую – обратной.
Приведем пример.
Прямая теорема. Если треугольник прямоугольный, то сумма квадратов его катетов равна квадрату гипотенузы. Обратная теорема. Если в некотором треугольнике сумма квадратов двух сторон равна квадрату третьей стороны, то такой треугольник прямоугольный.
Из двух взаимно обратных теорем  и
и 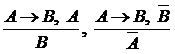 в общем случае каждая может оказаться верной или неверной. Например, пусть
в общем случае каждая может оказаться верной или неверной. Например, пусть  четырехугольник является параллелограммом},
четырехугольник является параллелограммом},  в четырехугольнике есть пара равных сторон}. Тогда теорема
в четырехугольнике есть пара равных сторон}. Тогда теорема  истинна, а
истинна, а 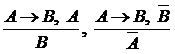 ложна.
ложна.
Если справедливы обе теоремы  и
и 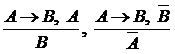 (прямая и обратная), то этот факт выражается сокращенной записью
(прямая и обратная), то этот факт выражается сокращенной записью . В этом случае говорят, что каждое из высказываний
. В этом случае говорят, что каждое из высказываний  является необходимым и достаточным условием для другого.
является необходимым и достаточным условием для другого.
Если в некоторой теореме  заменить и условие, и заключение их отрицаниями, то получится новая теорема
заменить и условие, и заключение их отрицаниями, то получится новая теорема  , которая называется противоположной исходной.
, которая называется противоположной исходной.
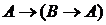 называется противоположной обратной теореме.
называется противоположной обратной теореме. Противоположная теорема – это теорема, условие и заключение которой являются отрицаниями условия и заключения данной теоремы.
Например, теорема, противоположная теореме Пифагора, может быть сформулирована так: если треугольник не прямоугольный, то квадрат любой его стороны не равен сумме квадратов двух других сторон.
Метод доказательства от противного. Ранее было отмечено, что высказывания  и
и 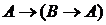 равносильны. Поэтому иногда для доказательства теоремы
равносильны. Поэтому иногда для доказательства теоремы  предполагают истинным высказывание
предполагают истинным высказывание  и пытаются вывести отсюда справедливость высказывания
и пытаются вывести отсюда справедливость высказывания  . Если это удается (т.е. будет доказана теорема
. Если это удается (т.е. будет доказана теорема 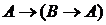 ), то исходную теорему
), то исходную теорему  тоже можно будет считать доказанной.
тоже можно будет считать доказанной.
При доказательстве утверждений различных математических теорий обычно используются рассуждения, которые на языке логики можно выразить формулами.