§1.7. Схемы из функциональных элементов
Каждой бинарной операции в алгебре логики соответствует функциональный элемент с двумя входами и одним выходом, унарной – с одним входом и одним выходом (см.
, то любую булеву функцию можно выразить формулой через функции полной системы и реализовать ее с помощью соответствующих ФЭ. Логическая схема 
, выходные сигналы 
которой описываются системой булевых функций
,
где 
входные сигналы логической схемы (
, 
), называется схемой из функциональных элементов (СФЭ).
Теорема. Для того, чтобы для произвольной системы
существовала схема из ФЭ с 
входами 
и 
выходами 
необходимо и достаточно, чтобы набор ФЭ соответствовал полной системе функций.
Обычно для построения схем используются базис 
(этот базис называется стандартным или булевым) или 
(базис Жегалкина).
Обозначим через 
функционал, равный числу элементов в схеме 
, означающий сложность схемы.
Проблема синтеза – построить схему с минимальной сложностью.
Решение типовых примеров
1. Представить формулой функцию, заданную схемой
Решение. Имеем: 
Отсюда
2. Построить схему, реализующую функцию
Решение. Положим 
Схема, реализующая функцию, выглядит так:
 |
 |
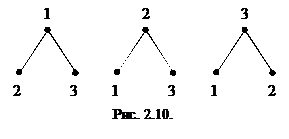
3. Упростить схему (рис. 1.10).
Решение. Требуется построить схему с меньшим числом функциональных элементов, реализующую ту же функцию 
Для этого выразим 
формулой и упростим формулу.
Следовательно, функция может быть реализована схемой из 2 функциональных элементов (рис. 1.11).
Задачи для самостоятельного решения
1. Представить формулой функцию, заданную схемой (рис. 1.12).
2. Представить схемой функцию 
 |
3. Упростить схему (рис. 1.13). Ответы
 |
1. 
(выражение не упрощено). 2. Схема изображена на рис. 1.14.
3. Схема изображена на рис. 1.15.
 |