§1.3. Реализация булевых функций формулами
Функция 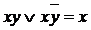 называется суперпозицией булевых функций
называется суперпозицией булевых функций  , если она получается некоторой подстановкой этих булевых функций друг в друга.
, если она получается некоторой подстановкой этих булевых функций друг в друга.
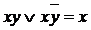 .
. Пусть  и
и  – две формулы. Говорят, что формулы
– две формулы. Говорят, что формулы  и
и  имеют одинаковое строение, если формула
имеют одинаковое строение, если формула  может быть получена из формулы
может быть получена из формулы  заменой каждого функционального символа
заменой каждого функционального символа  на символ
на символ  .
.
Пусть 
 . Формулой над
. Формулой над  является всякое (и только такое) выражение вида:
является всякое (и только такое) выражение вида:
(1)  – любая переменная из множества
– любая переменная из множества 
(2) 
 где
где  и
и  ранее построенные формулы над
ранее построенные формулы над  .
.
Обычно принимаются следующие соглашения для сокращения записи формул над множеством связок  :
:
а) внешние скобки у формул опускаются;
б) формула  записывается в виде
записывается в виде  ;
;
в) формула  записывается в виде
записывается в виде  или
или  ;
;
г) считается, что связка  сильнее любой двухместной связки из множества
сильнее любой двухместной связки из множества  ;
;
д) связка & считается сильнее любой другой двухместной связки из множества  .
.
На множестве переменных  введем функцию
введем функцию
 .
.
О формуле  , задающей функцию
, задающей функцию 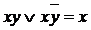 , говорят также, что формула
, говорят также, что формула  реализует функцию
реализует функцию 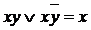 . Две формулы
. Две формулы  и
и  эквивалентны (
эквивалентны ( ), если реализуемые ими функции
), если реализуемые ими функции  и
и  равны.
равны.
В эквивалентности формул часто можно убедиться, построив таблицы соответствующих им функций.
Пример. Построив таблицы функций, выяснить эквивалентны ли формулы
 и
и  .
.
Решение. Построим векторы значений функций  и
и  .
.
Табл. 1.7
 |  |  |  |  |  |  |  |  |  |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
Из таблицы 1.7 видно, что  . Следовательно, формулы
. Следовательно, формулы  и
и  эквиваленты.
эквиваленты.