§2.4. Раскраски графов. Планарность
Пусть задано несколько красок  . Раскраской графа G называется правило, по которому каждой вершине графа присваивается номер
. Раскраской графа G называется правило, по которому каждой вершине графа присваивается номер  , соответствующий краске, причем смежные вершины имеют разные номера.
, соответствующий краске, причем смежные вершины имеют разные номера.
Хроматическим числом  графа G называется наименьшее число красок, требуемое для раскраски данного графа.
графа G называется наименьшее число красок, требуемое для раскраски данного графа.
Для полного графа  .
.
Граф называется бихроматичным, если для его раскраски требуется две краски ( ).
).
Теорема (Критерий бихроматичности). Для любого графа G эквивалентны условия:
(1) граф G бихроматичен;
(2) граф G двудольный;
(3) в графе G нет циклов нечетной длины.
Доказательство. Будем доказывать эквивалентность по схеме  .
.
 Пусть граф G бихроматичен. Нужно доказать, что в нем нет циклов нечетной длины. Предположим, что цикл нечетной длины существует:
Пусть граф G бихроматичен. Нужно доказать, что в нем нет циклов нечетной длины. Предположим, что цикл нечетной длины существует:  . В силу бихроматичности нечетные вершины одного цвета. Следовательно, вершины
. В силу бихроматичности нечетные вершины одного цвета. Следовательно, вершины  и
и  одного цвета, но они смежные. Получили противоречие. Циклов нечетной длины нет.
одного цвета, но они смежные. Получили противоречие. Циклов нечетной длины нет.
 Пусть в графе G нет циклов нечетной длины. Нужно доказать, что G двудольный. Пусть
Пусть в графе G нет циклов нечетной длины. Нужно доказать, что G двудольный. Пусть  – компоненты связности графа G.
– компоненты связности графа G.
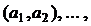 , если существует путь четной длины из вершины
, если существует путь четной длины из вершины 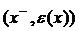 в вершину
в вершину 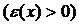 . Если из
. Если из 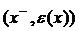 в
в 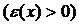 существует путь четной длины, то из
существует путь четной длины, то из 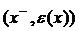 в
в 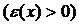 не существует пути нечетной длины, иначе нашелся бы цикл нечетной длины.
не существует пути нечетной длины, иначе нашелся бы цикл нечетной длины. Докажем, что “~” – отношение эквивалентности. Действительно, оно рефлексивно:  (из
(из 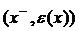 в
в 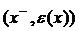 существует путь длины 0); симметрично: если
существует путь длины 0); симметрично: если 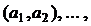 , то
, то  (если из
(если из 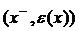 в
в 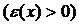 существует путь четной длины, то существует путь четной длины из
существует путь четной длины, то существует путь четной длины из 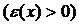 в
в 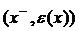 ); транзитивно: если
); транзитивно: если 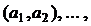 и
и  , то
, то  (если существует пути четной длины из
(если существует пути четной длины из 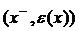 в
в 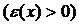 и из
и из 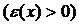 в
в  , то существует пути четной длины из
, то существует пути четной длины из 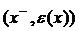 в
в  .
.
 Пусть G – двудольный граф. Нужно доказать, что он бихроматичен. Так как смежные вершины графа принадлежат разным долям, то вершины одной доли раскрасим в один цвет, второй – в другой. Теорема доказана.
Пусть G – двудольный граф. Нужно доказать, что он бихроматичен. Так как смежные вершины графа принадлежат разным долям, то вершины одной доли раскрасим в один цвет, второй – в другой. Теорема доказана.
Реберным хроматическим числом  графа G называется наименьшее количество красок, необходимых для раскраски ребер графа таким образом, чтобы смежные ребра имели разные цвета.
графа G называется наименьшее количество красок, необходимых для раскраски ребер графа таким образом, чтобы смежные ребра имели разные цвета.
Для полных графов 
Если  то, очевидно,
то, очевидно,  .
.
Справедлива теорема Визинга.  .
.