§3.3. Продолжение функций и
Пусть  конечный алфавит. Обозначим через
конечный алфавит. Обозначим через  множество всех слов
множество всех слов  Число
Число  называется длиной слова
называется длиной слова  и обозначается
и обозначается  Например, если
Например, если  то
то 

 Слово, в котором нет ни одной буквы, будем называть пустым словом и обозначать символом
Слово, в котором нет ни одной буквы, будем называть пустым словом и обозначать символом  Очевидно,
Очевидно,  Пусть
Пусть  множество всех слов длины
множество всех слов длины  а
а  множество всех непустых слов.
множество всех непустых слов.
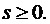 . Очевидно,
. Очевидно, 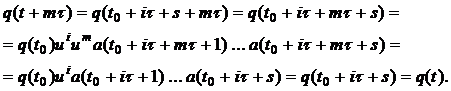
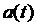
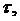
Произведением двух слов  называется слово, полученное приписыванием к слову
называется слово, полученное приписыванием к слову  справа слова
справа слова  Таким образом, если
Таким образом, если 
 то
то  Нетрудно проверить, что произведение слов ассоциативно, т.е.
Нетрудно проверить, что произведение слов ассоциативно, т.е.
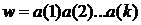 для любых
для любых 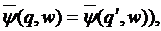 Вообще, произведение слов
Вообще, произведение слов 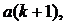 не зависит от расстановки скобок (но зависит от порядка сомножителей). В частности,
не зависит от расстановки скобок (но зависит от порядка сомножителей). В частности, 

Произведение слов некоммутативно, так как в общем случае 
Множество, на котором задана ассоциативная операция, называется полугруппой. Полугруппа  в которой есть единица, т.е. такой элемент е, что
в которой есть единица, т.е. такой элемент е, что  для всех
для всех  называется моноидом. Множества
называется моноидом. Множества  и
и  являются полугруппами. Кроме того,
являются полугруппами. Кроме того,  моноид (так как
моноид (так как  для всех
для всех  то пустое слово
то пустое слово  является единицей). Полугруппа
является единицей). Полугруппа  моноидом не является. Действительно, если
моноидом не является. Действительно, если  при некоторых
при некоторых  , то
, то  , откуда
, откуда  , что невозможно, так как
, что невозможно, так как  .
.
Функции  и
и  можно продолжить до функций
можно продолжить до функций  и
и  следующим образом. Положим
следующим образом. Положим
 при
при 
 при
при 

 при
при 
 при
при 



Функция  несёт информацию о том, в какое состояние перейдёт автомат, если на его вход будут поступать последовательно несколько букв из алфавита
несёт информацию о том, в какое состояние перейдёт автомат, если на его вход будут поступать последовательно несколько букв из алфавита  Действительно, если в какой-либо момент автомат находится в состоянии
Действительно, если в какой-либо момент автомат находится в состоянии  а на его вход поступают буквы
а на его вход поступают буквы  то будут осуществляться следующие переходы в другие состояния:
то будут осуществляться следующие переходы в другие состояния:


т.е. в конце концов автомат окажется в состоянии  Аналогичным образом интерпретируется функция
Аналогичным образом интерпретируется функция  А именно,
А именно,  где
где  буква, которая будет выдана автоматом на
буква, которая будет выдана автоматом на  -м шаге.
-м шаге.
Пример 1. Автомат задан таблицей 3.5.
 Определить:
Определить: 




Решение. 



поэтому



поэтому 
 Пример 2. Автомат задан диаграммой Мура, изображенной на рис. 3.12. Найти:
Пример 2. Автомат задан диаграммой Мура, изображенной на рис. 3.12. Найти:  ,
,  .
.
Решение. Имеем:

поэтому 


Задачи для самостоятельного решения
 1. Автомат задан таблицей 3.6. Найти: а)
1. Автомат задан таблицей 3.6. Найти: а)  б)
б) 
2.
Автомат задан диаграммой Мура, изображенной на рис. 3.13.Найти: а)  б)
б)  в)
в) 
г) 
3. Автомат задан каноническими уравнениями

где  и вычисления производятся по модулю 3. Найти: а)
и вычисления производятся по модулю 3. Найти: а)  , б)
, б)  . Ответы:
. Ответы:
1. а)  б)
б)  2. а)
2. а)  б)
б)  в)
в)  г)
г)  3. а) 2;
3. а) 2;
б) 0020.