§3.4. Приведённый автомат
Назовём состояния  и
и  автомата
автомата  неотличимыми, если
неотличимыми, если  для всех
для всех 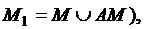 Состояния
Состояния  и
и  отличимы, если
отличимы, если  при некотором
при некотором 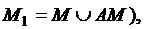 Положим
Положим  если
если  и
и  неотличичимы.
неотличичимы.
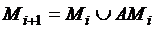 состояний автомата
состояний автомата 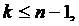 является отношением эквивалентности. Это отношение вызывает разбиение множества
является отношением эквивалентности. Это отношение вызывает разбиение множества 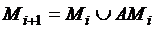 на непересекающиеся классы эквивалентности:
на непересекающиеся классы эквивалентности: 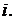 При этом любые два состояния
При этом любые два состояния 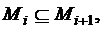 лежащие в одном классе, неотличимы, а любые два состояния из разных классов отличимы.
лежащие в одном классе, неотличимы, а любые два состояния из разных классов отличимы. Множество классов отношения ~ (фактор-множество  обозначим через
обозначим через  Построим новый автомат
Построим новый автомат  В качестве входного и выходного алфавитов автомата
В качестве входного и выходного алфавитов автомата  возьмём те же множества
возьмём те же множества  и
и  которые были у автомата
которые были у автомата  а в качестве множества состояний возьмём множество
а в качестве множества состояний возьмём множество  Надо определить теперь функции
Надо определить теперь функции  и
и 
Пусть 
 Наиболее естественным является следующее определение значения
Наиболее естественным является следующее определение значения  взять какой-нибудь элемент
взять какой-нибудь элемент  принадлежащий классу
принадлежащий классу  найти
найти  а затем класс, в котором лежит элемент
а затем класс, в котором лежит элемент  объявить значением
объявить значением  То есть считать, что
То есть считать, что

 (1)
(1)
Докажем корректность этого определения, т.е.
независимость от выбора представителя в классе эквивалентности. Пусть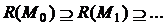 Определение будет некорректным, если окажется, что
Определение будет некорректным, если окажется, что 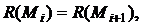 Докажем, что определение корректно. Если
Докажем, что определение корректно. Если 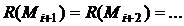 то
то 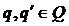 при некотором
при некотором 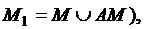 Это означает, что
Это означает, что 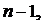 Следовательно,
Следовательно, 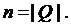 что противоречит условию. Итак,
что противоречит условию. Итак, 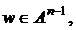 поэтому определение (1) корректно.
поэтому определение (1) корректно. Функцию  определим на
определим на  по формуле
по формуле
 (2)
(2)
По определению неотличимости состояний мы имеем  поэтому определение (2) корректно.
поэтому определение (2) корректно.
Автомат  называется приведённым автоматом, соответствующим автомату
называется приведённым автоматом, соответствующим автомату 
Докажем, что у приведённого автомата все состояния отличимы друг от друга. Пусть  Тогда
Тогда  для всех
для всех 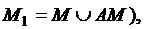 Отсюда по формуле (2) получаем, что
Отсюда по формуле (2) получаем, что  при всех
при всех 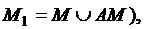 Следовательно,
Следовательно, 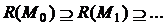 Отсюда следует, что
Отсюда следует, что  Итак, у автомата
Итак, у автомата  неотличимыми являются только совпадающие друг с другом состояния.
неотличимыми являются только совпадающие друг с другом состояния.
Автомат  и приведённый автомат
и приведённый автомат  работают одинаково: для любой входной последовательности
работают одинаково: для любой входной последовательности  последовательность
последовательность  на выходе автомата
на выходе автомата  и автомата
и автомата  одна и та же:
одна и та же: 
 и т.д. (здесь
и т.д. (здесь  начальное состояние). Решение типовых задач
начальное состояние). Решение типовых задач
Пример 1. Построить приведённый автомат для автомата, заданного следующей диаграммой Мура, изображенной на рис. 3.14.
Решение. Вычислим:  ,
,  ,
,  ,
,  ,
,  . Следовательно, состояние
. Следовательно, состояние  отличимо от всех остальных. Мы получаем (пока) следующее разбиение множества
отличимо от всех остальных. Мы получаем (пока) следующее разбиение множества  на классы, т.е. непересекающиеся подмножества:
на классы, т.е. непересекающиеся подмножества:  (далее это разбиение будет измельчаться).
(далее это разбиение будет измельчаться).
 Далее вычисляем:
Далее вычисляем: 


 Отсюда следует, что
Отсюда следует, что  не может лежать в одном классе с
не может лежать в одном классе с  или
или 
 с
с  или
или  и т.д.
и т.д.
 Положим
Положим 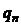
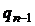
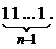 Покажем, что это окончательное разбиение. Имеем:
Покажем, что это окончательное разбиение. Имеем: 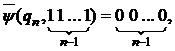
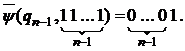 поэтому
поэтому 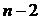 Аналогично получаем
Аналогично получаем 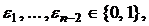 и т.д., т.е. функция
и т.д., т.е. функция 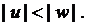 “не разбивает” классы. Следовательно, классы
“не разбивает” классы. Следовательно, классы 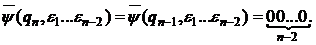 можно считать состояниями нового автомата. Это и есть приведённый автомат, его диаграмма Мура изображена на рисунке 3.15.
можно считать состояниями нового автомата. Это и есть приведённый автомат, его диаграмма Мура изображена на рисунке 3.15.
 |
 |
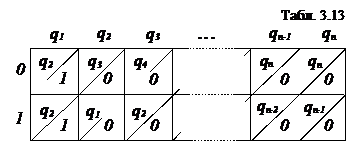
Пример 2. Построить приведённый автомат для автомата  , заданного следующей таблицей 3.7:
, заданного следующей таблицей 3.7:
 Решение. Верхняя строка таблицы 11011 определяет разбиение
Решение. Верхняя строка таблицы 11011 определяет разбиение  нижняя строка - разбиение
нижняя строка - разбиение  Их пересечение
Их пересечение  это разбиение
это разбиение  Докажем, что состояния
Докажем, что состояния 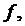 неотличимы друг от друга.
неотличимы друг от друга.
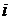 значит, функция
значит, функция 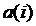 на состояниях
на состояниях 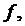 принимает одинаковые значения. Кроме того, другая часть столбцов:
принимает одинаковые значения. Кроме того, другая часть столбцов: 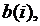 такова, что
такова, что 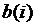 лежат в одном классе разбиения. Это доказывает, что
лежат в одном классе разбиения. Это доказывает, что 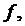 неотличимы. Из таблицы автомата
неотличимы. Из таблицы автомата 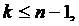 теперь нетрудно получить таблицу приведённого автомата
теперь нетрудно получить таблицу приведённого автомата 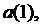 для этого достаточно взять по одному представителю в каждом классе разбиения
для этого достаточно взять по одному представителю в каждом классе разбиения 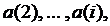 Таким образом, мы получаем таблицу 3.8:
Таким образом, мы получаем таблицу 3.8:Задачи для самостоятельного решения

1. Автомат 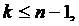 задан диаграммой Мура. Построить диаграмму Мура приведённого автомата
задан диаграммой Мура. Построить диаграмму Мура приведённого автомата 
 |
2. Автомат 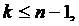 задан таблицей. Построить таблицу приведённого автомата
задан таблицей. Построить таблицу приведённого автомата 
Ответы
 |
1.
 |
2.