Примеры решения задач
 1. Построить максимальный поток в сети, изображённой на рисунке 2.78, и найти разрез, пропускная способность которого равна величине потока.
1. Построить максимальный поток в сети, изображённой на рисунке 2.78, и найти разрез, пропускная способность которого равна величине потока.
Решение. Вначале положим для всех рёбер  Двигаясь от вершины
Двигаясь от вершины  будем расставлять пометки (см. рис. 2.79).
будем расставлять пометки (см. рис. 2.79).
 Так как вершина
Так как вершина  оказалась помеченной, то можно величину потока увеличить. Вдоль пути
оказалась помеченной, то можно величину потока увеличить. Вдоль пути  увеличим поток через рёбра этого пути на
увеличим поток через рёбра этого пути на  Тогда получим распределение потока через рёбра, изображённое на рис. 2.80.
Тогда получим распределение потока через рёбра, изображённое на рис. 2.80.

Снова расставляем метки – см. рис. 2.81. Затем вдоль пути  увеличиваем поток через рёбра на
увеличиваем поток через рёбра на  (рис. 2.82). Расставляем метки ещё раз (см. рис. 2.83). Теперь “добраться” до вершины
(рис. 2.82). Расставляем метки ещё раз (см. рис. 2.83). Теперь “добраться” до вершины  невозможно. Значит, поток является
невозможно. Значит, поток является  максимальным. Его величина равна
максимальным. Его величина равна  Пусть
Пусть  (множество вершин, до которых можно “добраться” из
(множество вершин, до которых можно “добраться” из 
 оставшиеся вершины.
оставшиеся вершины.
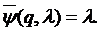 имеем:
имеем: 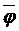 Значит,
Значит, 
2. Проверить, является ли поток в сети максимальным:
 |
Решение. Так как существует путь  в котором
в котором  для прямых стрелок и
для прямых стрелок и  для обратной стрелки, то поток не максимальный. Его можно увеличить на число
для обратной стрелки, то поток не максимальный. Его можно увеличить на число 
Задачи для самостоятельного решения
 1. Построить максимальный поток в сети, рассматривая пути
1. Построить максимальный поток в сети, рассматривая пути 





2. Построить максимальный поток в сети. Найти какой-либо разрез, пропускная способность которого равна величине потока: а) см. рис. 2.86; б) см. рис. 2.87.
3. Найти величину максимального потока в сети:
а) см. рис. 2.88;
 |
б) см. рис. 2.89.

 4.
4.
Ответы
 1.
1.
2. а) см. рис. 2.92, разрез: 

 |
б) см. рис. 2.93, разрез: 
 (ответ неоднозначен);
(ответ неоднозначен);
 |
3. а)  б)
б)  4. См. рис. 2.94.
4. См. рис. 2.94.