§2.5. Потоки в сетях
Транспортные, электрические, водопроводные и многие другие сети могут быть описаны на языке теории графов и с её помощью решены некоторые оптимизационные задачи.
Сеть – это ориентированный связный граф, рёбра которого помечены положительными действительными числами 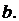 (для ребра
(для ребра  идущего из вершины
идущего из вершины  в вершину
в вершину  В графе должны быть выделены вершины
В графе должны быть выделены вершины  (источник) и
(источник) и  (сток).
(сток).
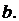 называется пропускной способностью ребра
называется пропускной способностью ребра 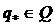
В сети допускаются кратные рёбра, но не допускаются петли. Вершины сети часто называют узлами.
Поток в сети – это функция  определённая для каждого ребра
определённая для каждого ребра  и удовлетворяющая условиям:
и удовлетворяющая условиям:
(а)  для любого ребра
для любого ребра 
(б) существует число  такое, что
такое, что

Число  называется величиной потока
называется величиной потока  Иногда пишут
Иногда пишут  вместо
вместо  чтобы подчеркнуть зависимость
чтобы подчеркнуть зависимость  от
от  Величина потока выражает количество субстанции (воды, или количества электричества, или автомашин), “перетекающих” из
Величина потока выражает количество субстанции (воды, или количества электричества, или автомашин), “перетекающих” из  в
в  за определённый промежуток времени.
за определённый промежуток времени.
 для внутренней точки
для внутренней точки 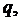 – это “закон сохранения” (сколько единиц субстанции “втекает” в узел
– это “закон сохранения” (сколько единиц субстанции “втекает” в узел 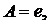 столько и “вытекает” из него). В математике рассматриваются и более общие сети – сети, имеющие несколько источников
столько и “вытекает” из него). В математике рассматриваются и более общие сети – сети, имеющие несколько источников 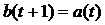 и несколько стоков
и несколько стоков 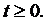
Поток  называется максимальным, если его величина
называется максимальным, если его величина  максимальна.
максимальна.
Основная задача теории потоков в сетях состоит в нахождении максимального потока. Мы покажем, что максимальный поток всегда существует, и приведём алгоритм его нахождения.
Теорема. В любой сети существует максимальный поток.
Доказательство. Пусть  все рёбра сети. Положим
все рёбра сети. Положим  Если
Если  поток, то полагаем
поток, то полагаем  Тогда поток
Тогда поток  можно отождествить с точкой
можно отождествить с точкой  п-мерного пространства
п-мерного пространства  Конечно, не всякая точка из
Конечно, не всякая точка из  определяет поток. Должно быть выполнено условие (а):
определяет поток. Должно быть выполнено условие (а):  т.е.
т.е.  (точка
(точка  лежит в параллелепипеде
лежит в параллелепипеде  ).
).
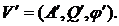 и
и 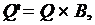 при
при 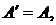 Например, если
Например, если 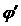 и сеть вблизи узла
и сеть вблизи узла 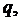 имеет вид
имеет вид
 |
то  Множество
Множество  всех точек
всех точек  , удовлетворяющих условиям (а) и (б), таким образом, является замкнутым и ограниченным (т.е. компактом) в
, удовлетворяющих условиям (а) и (б), таким образом, является замкнутым и ограниченным (т.е. компактом) в  . Величина потока
. Величина потока  является непрерывной функцией от
является непрерывной функцией от  определённой на компакте
определённой на компакте  (действительно,
(действительно,  линейная функция; здесь
линейная функция; здесь  ребра, выходящие из
ребра, выходящие из  а
а  входящие в
входящие в  По известной теореме математического анализа функция, непрерывная на компакте
По известной теореме математического анализа функция, непрерывная на компакте достигает своего наибольшего значения в некоторой точке из
достигает своего наибольшего значения в некоторой точке из  В нашем случае эта точка и будет давать максимальный поток.
В нашем случае эта точка и будет давать максимальный поток.
Введём ещё несколько обозначений. Пусть  множество всех узлов сети. Для двух подмножеств
множество всех узлов сети. Для двух подмножеств  положим
положим 
 Очевидно,
Очевидно,  при
при  и аналогичное равенство имеет место для функции
и аналогичное равенство имеет место для функции  Введём ещё одно понятие.
Введём ещё одно понятие.
Разрез – это разбиение множества  всех узлов сети на два непересекающихся подмножества
всех узлов сети на два непересекающихся подмножества  и
и  причём
причём  а
а  Число
Число  называется пропускной способностью разреза
называется пропускной способностью разреза 
 |
Пример. В сети, изображённой на рисунке 2.72, на каждом ребре  написаны числа
написаны числа 
 (пропускная способность этого ребра и поток через него). В этом примере величина потока
(пропускная способность этого ребра и поток через него). В этом примере величина потока  Этот поток не максимальный, так как можно, например, вдоль пути
Этот поток не максимальный, так как можно, например, вдоль пути  увеличить поток через рёбра на 1, условия (а) и (б) будут выполняться, но уже с
увеличить поток через рёбра на 1, условия (а) и (б) будут выполняться, но уже с  Рассмотрим разрез
Рассмотрим разрез  где
где 
 Его пропускная способность равна
Его пропускная способность равна  Мы имеем:
Мы имеем: 
 |
Оказывается, такое неравенство выполняется во всякой сети для любого потока и любого разреза.
Сформулируем этот факт в виде леммы, которая потребуется затем для доказательства основной теоремы.Лемма. Величина любого потока в сети не превосходит пропускной способности любого разреза, т.е. 
Доказательство. Пусть  поток и
поток и  разрез. Пусть
разрез. Пусть  множество всех узлов сети. По определению потока имеем:
множество всех узлов сети. По определению потока имеем: 
 при
при 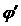 и
и  Складывая выражения
Складывая выражения  для
для  и учитывая, что
и учитывая, что 
 получим:
получим:  Отсюда следует, что
Отсюда следует, что


 ,
,
так как  Лемма доказана.
Лемма доказана.
Итак, величина любого потока меньше или равна пропускной способности любого разреза. Поэтому, если мы найдём поток и разрез, для которых  то поток будет максимальным (а разрез – минимальным). На этом простом замечании основаны алгоритм построения максимального потока и основная теорема о максимальном потоке, к изложению которых мы сейчас переходим.
то поток будет максимальным (а разрез – минимальным). На этом простом замечании основаны алгоритм построения максимального потока и основная теорема о максимальном потоке, к изложению которых мы сейчас переходим.
Алгоритм построения максимального потока в сети.
1-й шаг. Полагаем для каждого ребра  данной сети
данной сети 
2-й шаг. Будем просматривать узлы сети и расставлять на них пометки вида  или
или 
 по следующему принципу. Источнику
по следующему принципу. Источнику  присваиваем метку
присваиваем метку  Если вершина
Если вершина 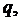 уже помечена, а вершина
уже помечена, а вершина  ещё нет, то мы помечаем вершину
ещё нет, то мы помечаем вершину  в следующих случаях:
в следующих случаях:
 если есть ребро из
если есть ребро из 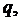 в
в  и
и 
 если есть ребро из
если есть ребро из  в
в 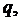 и
и 
В случае  вершина
вершина  получает метку
получает метку  где
где  в случае
в случае  метку
метку  где
где 
 |
Просмотр вершин и расстановку меток будем продолжать, пока это возможно. При этом могут представиться следующие случаи:
(1) вершина  оказалась помеченной;
оказалась помеченной;
(2) вершина  не помечена, но больше никакие вершины пометить невозможно.
не помечена, но больше никакие вершины пометить невозможно.
Покажем, что в случае (1) величину потока можно увеличить, а в случае (2) построенный поток является максимальным. Действительно, пусть имеет место случай (1). Тогда в процессе расстановки меток можно будет “добраться” из  в
в  Следовательно, существует путь
Следовательно, существует путь 

 состоящий из помеченных вершин. Будем считать, что вершины этого пути взяты в “хронологическом” порядке (т.е. в порядке, в котором расставлялись метки). Некоторые из стрелок
состоящий из помеченных вершин. Будем считать, что вершины этого пути взяты в “хронологическом” порядке (т.е. в порядке, в котором расставлялись метки). Некоторые из стрелок  прямые, а некоторые обратные (см. рис 2.74).
прямые, а некоторые обратные (см. рис 2.74).
 |
Метки для прямых и обратных стрелок выглядят так, как показано на рис. 2.75.
 |
Из принципа расстановки меток видно, что 
3-й шаг. Увеличим величину потока  на число
на число  прибавив
прибавив  к потоку
к потоку  для прямых рёбер и отняв
для прямых рёбер и отняв  от
от  для обратных рёбер (см. рис. 2.76).
для обратных рёбер (см. рис. 2.76).
Условия (а) и (б) при этом не нарушатся, и мы получим поток величины  После этого стираем все метки и начинаем расстановку меток заново, т.е. возвращаемся к шагу 2.
После этого стираем все метки и начинаем расстановку меток заново, т.е. возвращаемся к шагу 2.
Пусть теперь имеет место случай (2), т.е. в процессе расстановки меток “добраться” до вершины  невозможно. Докажем, что в этом случае алгоритм можно считать завершённым, так как построенный поток уже максимальный. Обозначим через
невозможно. Докажем, что в этом случае алгоритм можно считать завершённым, так как построенный поток уже максимальный. Обозначим через  множество всех помеченных вершин, а
множество всех помеченных вершин, а  непомеченных. Очевидно,
непомеченных. Очевидно,  разрез. Покажем, что для стрелок из
разрез. Покажем, что для стрелок из  в
в  имеет место равенство
имеет место равенство  а для стрелок из
а для стрелок из  в
в  равенство
равенство 
Действительно, пусть 
 Если
Если  то вершина
то вершина  может быть помечена меткой
может быть помечена меткой  поэтому
поэтому  что невозможно. А если
что невозможно. А если  то вершина
то вершина  получает метку
получает метку  поэтому
поэтому  что невозможно. Для данного разреза
что невозможно. Для данного разреза  мы имеем:
мы имеем:
 |

Так как величина потока равна пропускной способности разреза, то поток максимальный.
Проверим теперь эффективность этого алгоритма, т.е. тот факт, что, применяя его, за конечное число итераций будет построен максимальный поток. Проверку осуществим для случая, когда все пропускные способности 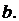 являются рациональными числами. Это ограничение не носит принципиального характера, так как действительное число можно приблизить с любой степенью точности рациональным числом, а при реализации на компьютере действия и так проводятся лишь с рациональными числами. Заметим, что наш алгоритм монотонный в том смысле, что величина потока
являются рациональными числами. Это ограничение не носит принципиального характера, так как действительное число можно приблизить с любой степенью точности рациональным числом, а при реализации на компьютере действия и так проводятся лишь с рациональными числами. Заметим, что наш алгоритм монотонный в том смысле, что величина потока  в ходе алгоритма постоянно увеличивается. Так как числа
в ходе алгоритма постоянно увеличивается. Так как числа 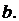 рациональны, то можно их привести к общему знаменателю, а затем умножить на знаменатель; 7таким образом, можно считать, что все
рациональны, то можно их привести к общему знаменателю, а затем умножить на знаменатель; 7таким образом, можно считать, что все  целые числа. В ходе работы алгоритма числа
целые числа. В ходе работы алгоритма числа  будут также получаться целыми, а значит, и числа
будут также получаться целыми, а значит, и числа  целые. Монотонность алгоритма означает, что
целые. Монотонность алгоритма означает, что  (
( величина потока на i-й итерации алгоритма). Очевидно, последовательность
величина потока на i-й итерации алгоритма). Очевидно, последовательность  ограниченная. Так как члены последовательности – целые числа, то величина
ограниченная. Так как члены последовательности – целые числа, то величина  достигнет своего наибольшего значения, а значит, алгоритм будет завершён.
достигнет своего наибольшего значения, а значит, алгоритм будет завершён.
Из алгоритма нахождения максимального потока и леммы следует основная теорема о потоках в сетях:
Теорема Форда – Фалкерсона. Для всякой сети существуют поток  и разрез
и разрез  такие, что величина потока равна пропускной способности разреза:
такие, что величина потока равна пропускной способности разреза:  В этом случае поток
В этом случае поток  максимальный.
максимальный.