§3.5. Периодичность выходной последовательности конечного автомата
Мы докажем, что любой конечный автомат перерабатывает периодическую входную последовательность в периодическую выходную, период которой не превышает 
где 
период входной последовательности, а 
количество состояний автомата.
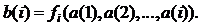а последовательность состояний автомата – период 
то выходная последовательность будет иметь период НОК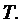
где НОК обозначает наименьшее общее кратное. В теореме этого раздела и во многих других вопросах теории автоматов будет удобно использовать сокращённые обозначения для функций 
и 
А именно, пусть 
автомат, 
и 
Если 
то этот факт мы будем записывать просто: 
Аналогично этому вместо записи 
будем использовать сокращённую запись 
Теорема.
Если входная последовательность конечного автомата является периодической, то выходная последовательность также периодическая.Доказательство. Пусть 
конечный автомат. Предположим, что на вход автомата поступает периодическая последовательность 
Если её период, то 
при 
где 
момент времени, с которого начинается период. Введём в рассмотрение следующие слова:
предпериод входной последовательности и
период. Пусть 
начальное состояние автомата. Положим 
Рассмотрим последовательность состояний 
Так как число членов этой последовательности равно 
то среди них есть совпадающие, т.е. существуют различные 
такие, что 
Можно считать, что 
Тогда 
где 
и 
Итак, 
Докажем теперь периодичность последовательности 
Пусть 
Тогда 
где 
Получаем:
По условию последовательность 
периодическая с периодом 
по только что доказанному 
периодическая с периодом 
Отсюда, используя канонические уравнения автомата, выведем периодичность выходной последовательности.
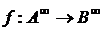то 
Теорема доказана.