Основные понятия и факты, связанные с булевым кубом
В дальнейшем в качестве множества  будет использоваться множество
будет использоваться множество  .
.
Набор  , где
, где  , называется булевым или двоичным набором (вектором). Элементы набора называют компонентами или координатами. Число
, называется булевым или двоичным набором (вектором). Элементы набора называют компонентами или координатами. Число  называют длиной набора. Кратко
называют длиной набора. Кратко  обозначают
обозначают  или
или  . Весом (или нормой) набора
. Весом (или нормой) набора  называют число его координат, равных 1, т.е.
называют число его координат, равных 1, т.е.  . Число
. Число  называют номером набора
называют номером набора  .
.
Замечание. Набор  есть разложение числа
есть разложение числа  в двоичной системе и находится следующим образом: а) делим
в двоичной системе и находится следующим образом: а) делим  на 2, остаток есть
на 2, остаток есть  частное
частное  ; б) делим
; б) делим  на 2, остаток есть
на 2, остаток есть  частное
частное  ; и т.
; и т.
Множество всех булевых векторов  длины
длины  называется
называется  -мерным кубом (
-мерным кубом ( ). Сами векторы называются вершинами
). Сами векторы называются вершинами  -мерного куба.
-мерного куба.
Кроме обозначения  для
для  -мерного куба используют обозначение
-мерного куба используют обозначение  , а наборы
, а наборы  называют вершинами куба
называют вершинами куба  .
.
 |
Геометрическая реализация. На рисунке 1.1. изображены проекции 1-мерного, 2-мерного, 3-мерного и 4-мерного кубов на плоскость.
Пусть  фиксированный набор чисел из 0 и 1 (
фиксированный набор чисел из 0 и 1 ( ). Множество всех вершин
). Множество всех вершин  куба
куба  таких, что
таких, что  , называется
, называется  -мерной гранью.
-мерной гранью.
Замечание.  -мерная грань является
-мерная грань является  -мерным подкубом куба
-мерным подкубом куба  .
.
Расстоянием (Хемминга) между вершинами  и
и  куба
куба  называется число
называется число  (т.е. число координат, в которых наборы
(т.е. число координат, в которых наборы  и
и  отличаются друг от друга).
отличаются друг от друга).
Вершины  и
и  куба
куба  – соседние, если
– соседние, если  , и противоположные; если
, и противоположные; если  .
.
Говорят, что набор  предшествует набору
предшествует набору  (обозначают
(обозначают  ), если
), если  для всех
для всех  . Если
. Если  и
и  , то говорят, что набор
, то говорят, что набор  строго предшествует набору
строго предшествует набору  и обозначают
и обозначают  . Наборы
. Наборы  и
и  называют сравнимыми, если либо
называют сравнимыми, если либо  либо
либо  .
.
Функция  такая, что
такая, что  , называется булевой функцией (или функцией алгебры логики) от
, называется булевой функцией (или функцией алгебры логики) от  переменных.
переменных.
Замечание. Булевы функции являются удобными для описания, анализа и синтеза переключательных схем, выходные сигналы которых характеризуются лишь двумя уровнями напряжения: высоким (1) и низким (0). Поэтому в практических приложениях их еще называют переключательными.
Для задания булевой функции  требуется указать ее значения на каждом наборе
требуется указать ее значения на каждом наборе  . При
. При  функцию
функцию  можно задать таблицей
можно задать таблицей  (табл. 1.1), называемой таблицей истинности функции, в которой наборы
(табл. 1.1), называемой таблицей истинности функции, в которой наборы  выписываются в порядке возрастания их номеров (сверху вниз).
выписываются в порядке возрастания их номеров (сверху вниз).
Табл. 1.1.
 |  |  |  |  |  |
| 0 | 0 |  | 0 | 0 |  |
| 0 | 0 |  | 1 | 1 |  |
| 0 | 0 |  | 1 | 0 |  |
 |  |  |  |  |  |
| 0 | 1 |  | 1 | 1 |  |
| 1 | 1 |  | 1 | 1 |  |
При стандартном расположении наборов (в соответствии с увеличением их номера), функцию  можно задавать вектором ее значений
можно задавать вектором ее значений  (или
(или  ), где координата
), где координата  равна значению функции
равна значению функции  в
в 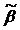 -ой строке таблицы (
-ой строке таблицы ( ), т.е.
), т.е.
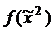 . При этом значение переменной
. При этом значение переменной 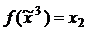
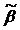 -ой строке таблицы есть компонента
-ой строке таблицы есть компонента 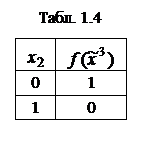 набора
набора 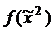 , которая определяются как соответствующая
, которая определяются как соответствующая  -я цифра в записи числа
-я цифра в записи числа 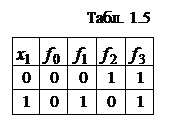 .
. Обозначим через  множество всех булевых функций от
множество всех булевых функций от  переменных, а
переменных, а  множество всех булевых функций.
множество всех булевых функций.
Теорема.  .
.
Доказательство. Поскольку функция  задается вектором значений
задается вектором значений  , где
, где  ,
,  , то различных булевых функций от
, то различных булевых функций от  переменных столько же, сколько различных
переменных столько же, сколько различных  -разрядных двоичных векторов, т.е.
-разрядных двоичных векторов, т.е.  .
.