Метрические характеристики графа
Пусть G – граф, а и и v – две его несовпадающие вершины. Длина кратчайшего (и, v)-маршрута (он, естественно, является простой цепью) называется расстоянием между вершинами и и v и обозначается через d(u, v).
Положим еще d(u, и) = 0. Очевидно, что введенное таким образом расстояние удовлетворяет аксиомам метрики:1) d(u, v) ? 0,
2) d(u, v) = 0 тогда и только тогда, когда u = v,
3) d(u, v) = d(v, u),
4) d(u, v) + d(v, w) ? d(u, w) (неравенство треугольника).
Для фиксированной вершины и величина

называется эксцентриситетом вершины и. Максимальный из всех эксцентриситетов вершин графа называется диаметром графа G и обозначается через d(G). Тем самым,
 .
.
|
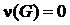 .
. Простая цепь длины d(G), расстояние между концами которой равно d(G), называется диаметральной цепью.
 Пример 4. В графе на рис. 2.15 d(1,2) = 1, d(1, 3) = 2; е(1) = 2; d(G) = 2. Все вершины, кроме вершины 2 являются периферийными, (1, 2, 3) – диаметральная цепь.
Пример 4. В графе на рис. 2.15 d(1,2) = 1, d(1, 3) = 2; е(1) = 2; d(G) = 2. Все вершины, кроме вершины 2 являются периферийными, (1, 2, 3) – диаметральная цепь.
Минимальный из эксцентриситетов вершин связного графа называется его радиусом и обозначается r(G):  .
.
Очевидно, что радиус графа не больше его диаметра.
Вершина  называется центральной, если
называется центральной, если  . Множество всех центральных вершин графа называется его центром. Граф может иметь единственную центральную вершину или несколько центральных вершин.
. Множество всех центральных вершин графа называется его центром. Граф может иметь единственную центральную вершину или несколько центральных вершин.
1. Доказать, что сумма степеней всех вершин графа равно удвоенному числу ребер (лемма о рукопожатиях):  .
.
Решение. Рассмотрим сумму степеней всех вершин графа. Каждое ребро вносит в эту сумму 1 два раза (оно учитывается в степенях двух вершин). Поэтому сумма степеней всех вершин графа равно удвоенному числу ребер.
2. Найти все неизоморфные графы четвертого порядка.
Решение. У графа четвертого порядка число ребер может быть от 0 в пустом графе О4 до 6 в полном графе K4.
Если  , получаем единственный граф О4.
, получаем единственный граф О4.
Если  – тоже единственный граф с двумя изолированными вершинами и двумя смежными друг другу.
– тоже единственный граф с двумя изолированными вершинами и двумя смежными друг другу.
При  получаем два графа: ребра смежные и нет.
получаем два графа: ребра смежные и нет.
При  имеем:
имеем:  . Если изолированных вершин нет, то возможные наборы степеней вершин: 1, 1, 2, 2 и 1, 1, 1, 3. Если изолированная вершина одна, то нет вершины со степенью 3, и возможный набор степеней вершин 2, 2, 2, т.е. цикл. Двух изолированных вершин быть не может.
. Если изолированных вершин нет, то возможные наборы степеней вершин: 1, 1, 2, 2 и 1, 1, 1, 3. Если изолированная вершина одна, то нет вершины со степенью 3, и возможный набор степеней вершин 2, 2, 2, т.е. цикл. Двух изолированных вершин быть не может.
Если  , получаем, что из полного графа удалены два ребра: либо смежные, либо нет. Получаем два графа.
, получаем, что из полного графа удалены два ребра: либо смежные, либо нет. Получаем два графа.
Если  получаем единственный граф удалением из полного графа одного ребра.
получаем единственный граф удалением из полного графа одного ребра.

Все неизоморфные графы порядка 4 представлены на рис. 2.16.
3. Доказать, что если число ребер графа порядка п > 2 больше, чем  , то он связен.
, то он связен.
Решение. Предположим, что он не связен. Тогда существуют две вершины а и b, не связанные между собой. Обозначим через V1 множество вершин, достижимых из  , а через V2 – множество вершин, достижимых из b. Тогда ни одна вершина из V2 не связана ни с какой вершиной из V1. Пусть |V1| = k < n, k > 0. Тогда | V2 | = n – k > 0. Если k = 1, то |V2| = n – 1 и наибольшее значение |E| равно
, а через V2 – множество вершин, достижимых из b. Тогда ни одна вершина из V2 не связана ни с какой вершиной из V1. Пусть |V1| = k < n, k > 0. Тогда | V2 | = n – k > 0. Если k = 1, то |V2| = n – 1 и наибольшее значение |E| равно  (когда подграф, порожденный V2 – полный), что противоречит условию. При k ? 2 наибольшее значение достигается, если подграфы, порожденные V1 и V2 – полные. Тогда,
(когда подграф, порожденный V2 – полный), что противоречит условию. При k ? 2 наибольшее значение достигается, если подграфы, порожденные V1 и V2 – полные. Тогда,  , и для всего графа имеем
, и для всего графа имеем 
 ,
,
что противоречит условию, следовательно, исходный граф связен.
4. Доказать, что в связном графе любые две простые цепи максимальной длины имеют общую вершину.
Решение. Предположим, что у двух простых цепей  и
и  максимальной длины нет общих вершин. Возьмем произвольно по одной вершине из каждой цепи
максимальной длины нет общих вершин. Возьмем произвольно по одной вершине из каждой цепи 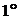 и
и 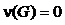 . Так как граф связный, то существует путь из
. Так как граф связный, то существует путь из 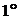 в
в 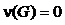 . Выберем из отрезков цепей от
. Выберем из отрезков цепей от  до
до 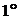 и от
и от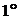 до
до  тот, длина которого не меньше
тот, длина которого не меньше  .
.
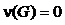 . Составим новую простую цепь из этих отрезков и простой цепи, соединяющей
. Составим новую простую цепь из этих отрезков и простой цепи, соединяющей 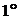 и
и 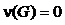 , ее длина больше
, ее длина больше 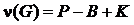 , что противоречит тому, что исходные цепи максимальны. Задачи для самостоятельного решения
, что противоречит тому, что исходные цепи максимальны. Задачи для самостоятельного решения 1. Доказать, что число ребер в полном графе Кп порядка п равно  .
.
2. Найти |V(Bn)|, |E(Bn)|, где Bn – п-мерный куб.
3. Найти количество неизоморфных графов, имеющих 7 вершин и 20 ребер.
4. Найти количество неизоморфных графов, имеющих 10 вершин и 43 ребра.
5. Найти все попарно неизоморфные графы пятого порядка.
6. Найти число помеченных графов, имеющих п вершин и т ребер.
7. Доказать, что если порядок самодополнительного графа равен п, то п º 0 (mod 4) или п º 1 (mod 4).
8. Найти самодополнительный граф с минимальным, отличным от 1 числом вершин.
9.
 |
Изобразить граф, являющийся дополнением графа G (рис. 2.17).
10. Доказать, что не существует графа, степени всех вершин которого попарно различны.
11. Существует ли граф со следующим набором степеней вершин:
а)1, 1, 1, 3, 3, 4, 4;
б)1, 1, 2, 2, 2, 3, 3, 4?
Определяется ли граф однозначно набором степеней вершин?
12. Построить граф с данным набором степеней вершин:
а)1, 1, 2, 2, 2;
б) 1, 2, 2, 2, 3, 4.
13. Доказать, что в любом графе число вершин нечетной степени четно.
14. Существует ли граф с шестью вершинами, у которого степени всех вершин равны 3?
15. Доказать, что любой путь, соединяющий вершины u и v, содержит простую цепь, соединяющую те же вершины.
16. Сколько существует путей длины 3 из вершины (0, 0, 0) в (1, 1, 1) в графе В3?
17. Доказать, что в двух простых цепях максимальной длины связного графа совпадают средние вершины, если 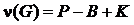 – четное, и одна из двух средних вершин одной цепи совпадает с одной из двух средних вершин другой цепи, если
– четное, и одна из двух средних вершин одной цепи совпадает с одной из двух средних вершин другой цепи, если  – нечетное.
– нечетное.
18. Привести пример цикла, не являющегося простым.
19. Доказать, что всякий цикл содержит простой цикл.
20. Доказать, что объединение двух несовпадающих простых (u, v)-цепей содержит простой цикл.
21. Пусть С и D – два несовпадающих простых цикла, имеющих общее ребро е. Доказать, что граф (С ÈD)\ e содержит простой цикл.
22. Показать, что расстояние между вершинами графа удовлетворяет аксиомам метрики.
23. Доказать, что если d(G) ? (п – 1)/2, то граф G связен.
24. Построить граф, центр которого
а) состоит ровно из одной вершины;
б) состоит ровно из трех вершин и не совпадает с множеством всех вершин;
в) совпадает с множеством всех вершин.
25. Доказать, что диаметр графа не превосходит его удвоенного радиуса.
26. Привести пример графа, диаметр и радиус которого равны.
27. Найти расстояние d(u, v) в графе, изображенном на рис. 2.18.
28. Какие из пар графов на рис. 2.19 изоморфны?
29. Докажите, что отношение изоморфизма графов является отношением эквивалентности. 
 |
Ответы
1. Указание. Степень каждой вершины равна п – 1. Сумма степеней вершин равна удвоенному числу ребер. 2. |V(Bn)| = 2п, |E(Bn)| = п2п – 1.
3. 1. Указание: посчитать, сколько ребер удалено из полного графа.
4. 2. 5. Указание: рассмотреть возможные наборы степеней вершин.
6.  . Указание: рассмотреть полный граф и выяснить, скольким способами можно выбрать из него те ребра, которые остаются в искомом. 7. Указание: удвоенная сумма числа ребер графа равна числу ребер полного графа. 8. Указание: рассмотрев наборы степеней вершин, доказать, что среди графов порядка 4 самодополнительных нет и построить граф порядка 5. 10. Указание: предположить обратное для графа с п вершинами и доказать, что у одной вершины должна быть степень п. 11. а) Нет; б) Да. Не определяется. Указание: рассмотреть сумму степеней вершин. 13. Указание: рассмотреть сумму степеней вершин. 14. Существует. 15. Указание: если в путь входит одна и та же вершина, участок пути, заключенный между ее первым вхождением и последним, можно удалить. 16. 6.
. Указание: рассмотреть полный граф и выяснить, скольким способами можно выбрать из него те ребра, которые остаются в искомом. 7. Указание: удвоенная сумма числа ребер графа равна числу ребер полного графа. 8. Указание: рассмотрев наборы степеней вершин, доказать, что среди графов порядка 4 самодополнительных нет и построить граф порядка 5. 10. Указание: предположить обратное для графа с п вершинами и доказать, что у одной вершины должна быть степень п. 11. а) Нет; б) Да. Не определяется. Указание: рассмотреть сумму степеней вершин. 13. Указание: рассмотреть сумму степеней вершин. 14. Существует. 15. Указание: если в путь входит одна и та же вершина, участок пути, заключенный между ее первым вхождением и последним, можно удалить. 16. 6.
17. Указание: предположить, что не совпадают и построить цепь большей длины.
19. Указание: если в цикл входит одна и та же вершина, участок цикла, заключенный между ее первым вхождением и последним, можно удалить.
20. Указание: доказать, что объединение этих цепей является циклом. 21. Указание: доказать, что (С ÈD)\ e является циклом.
23. Указание: найти сумму степеней вершин.
25. Указание: предположить противное и найти вершины, расстояние между которыми превосходит диаметр. 27. 3. 28. а), б), г).