Метод Квайна
1. По  строим СДНФ. Например, для функции
строим СДНФ. Например, для функции  .
.
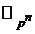 .
. 2. Применяем операцию неполного склеивания
 .
.
3. После того как такая операция применена к каждой паре конъюнкций из СДНФ, к которой она применима, с помощью операции поглощения ( ) удаляем те конъюнкции ранга
) удаляем те конъюнкции ранга  , которые можно удалить таким образом. В итоге получаем некоторую д. н. ф.
, которые можно удалить таким образом. В итоге получаем некоторую д. н. ф.  .
.
4. Если проведено  этапов, то на
этапов, то на  -м этапе операции неполного склеивания и поглощения применяются к конъюнкции ранга
-м этапе операции неполного склеивания и поглощения применяются к конъюнкции ранга  д. н. ф.
д. н. ф.  . Получаем д. н. ф.
. Получаем д. н. ф.  .
.
Алгоритм завершается, если  .
.
Пример. Построить сокращенную д. н. ф. функции
 .
.
Решение.  .
.
После первого этапа имеем  .
.
После второго этапа имеем  .
.
Простая импликанта  называется ядровой, если существует набор
называется ядровой, если существует набор  такой, что
такой, что  , но
, но  для всех
для всех  , входящих в сокращенную д.
, входящих в сокращенную д.
Геометрическая интерпретация:  – ядровая импликанта, если существует точка, принадлежащая
– ядровая импликанта, если существует точка, принадлежащая  , которая покрывается только
, которая покрывается только  .
.
Пример. Для функции  сокращенная д. н. ф. = =
сокращенная д. н. ф. = = .
.
Ядровая д. н. ф. (ЯДНФ) – это дизъюнкция всех ядровых импликант.
 |
Пример. На рис. 1.6 представлен носитель функции, у которой нет ядровой д. н. ф. Задачи для самостоятельного решения
1. Из заданного множества  элементарных конъюнкция выделить простые импликанты функции
элементарных конъюнкция выделить простые импликанты функции  :
:
а)  ;
;
б)  ;
;
в)  .
.
2. Построить сокращенную д. н. ф. по заданной к. н. ф.:
а)  ;
;
б)  .
.
3. Используя алгоритм Квайна, построить сокращенную д. н. ф. функции  :
:
а)  ; б)
; б)  .
.
4. Изобразив множество  функции
функции  в
в  , найти ее простые импликаты, построить сокращенную и ядровую д.
, найти ее простые импликаты, построить сокращенную и ядровую д.
а)  ;
;
б)  .
.
5. Найти длину сокращенной д. н. ф. функции  :
:
а)  ;
;
б)  .
.
6. Показать, что число функций, для которых фиксированная элементарная конъюнкция ранга  является импликантой, равно
является импликантой, равно  .
.
7. Показать, что любая функция от  переменных может быть реализована д. н. ф., содержащей не более
переменных может быть реализована д. н. ф., содержащей не более  элементарных конъюнкций.
элементарных конъюнкций.
8. Показать, что число конъюнкций в тупиковых д. н. ф. не превосходит  .
.
9. Показать, что число ядровых импликант функции  не превосходит
не превосходит  .
.
10. Показать, что вякая простая импликанта функции  :
:
а) ранга  является ядровой;
является ядровой;
б) ранга меньше 2 является ядровой. Ответы
1. а)  ; б)
; б)  ; в)
; в)  . 2. а)
. 2. а)  ;
;
б)  . 3. а)
. 3. а)  ; б)
; б) 
 . 4. а) сокращенная, она же ядровая д. н. ф.
. 4. а) сокращенная, она же ядровая д. н. ф.  ;
;
б)  сокращенная д. н. ф.,
сокращенная д. н. ф.,  ядровая д. н. ф. 5. а)
ядровая д. н. ф. 5. а)  ; б)
; б)  .
.