Изоморфизм графов
Легко подсчитать число графов с фиксированным множеством вершин V. Эти графы различаются своими ребрами, и поэтому их число равно количеству подмножеств множества V´V, т.е.
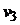, где п = | V |. Однако эти графы на всегда следует различать. Как в применении теории графов, так и в самой этой теории чаще существенно лишь то, что есть объекты (вершины графа) и связи между объектами (ребра графа). С этих позиций графы, которые получаются один из другого изменением наименований вершин, разумно не различать. Такие графы называются изоморфными. Пусть G и Н – графы, а 
– биекция. Если для любых вершин и и v графа G их образы 
и 
смежны в Н тогда и только тогда, когда и и v смежны в G, то эта биекция называется изоморфизмом графа G на граф Н. Если такой изоморфизм существует, то мы пишем 
и говорим, что графы G и Н изоморфны.
Пример 1. Графы, представленные на рис. 2.8 изоморфны, указана соответствующая изоморфизмам нумерация вершин. Графы на рис. 2.9 неизоморфны (например, вследствие того, что в первом графе есть циклы из трех ребер, а во втором их нет).
Очевидно, что отношение изоморфизма графов является эквивалентностью, т.е. оно симметрично, рефлексивно и транзитивно. Следовательно, все графы разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны.
В некоторых случаях приходится различать изоморфные графы. Граф порядка п называется помеченным, если его вершинам присвоены некоторые метки, например, номера 1, 2, …, п. Отождествив каждую из вершин графа с ее номером (а, следовательно, множество вершин – с множеством чисел {1, 2, …, п}), определим равенство графов G и Н одного и того же порядка: G = Н тогда, когда ЕG = ЕН. На рис. 2.10 изображены три разных помеченных графа.
Число gn помеченных графов порядка п определяется сложно. Известна формула Пойа
,
дающая асимптотику числа gn. Эта формула означает, что две функции g(п)=gn и f(n)=
асимптотически равны, т.е. 
.